Conceptual lens design by the masters, without using expensive software, but a spreadsheet

Introduction to the General Theme
About this guide (and how we can use a spreadsheet in lens design)
This guide will tackle how lens design was done before optical design software on computers were invented, which I will call the “classic” method for lens design. Although the calculation methods are classic, with the help of a spreadsheet, we will do a step-by-step lens design that makes all of the steps and theory make sense.
What you will learn in this guide, how we incorporate a spreadsheet
The basis of lens design, the refraction of light itself is a relatively simple concept that we can learn in physics class such as Snell’s Law, but lens design uses those concepts in a complex configurations that is a science to itself. How did the people in the past design a lens, before computers came into the lens design picture? Most calculated rays of light by hand. We can replicate this with a spreadsheet.

By learning the classic method to do lens design, we will be able to dig up the properties of lenses that are required for the lens system in a way that can be easily buried when using expensive, proprietary lens design software programs. Total system design require the software, but breaking the optical system down into intermediate lens groups, and understanding the choices of lenses that you are using is an acquired knowledge that can’t be learned by simply using the software.
Who this guide is for
- People who want to sharpen their existing lens design skills
- People who want the basic knowledge of lens design explained clearly, and visualized in a spreadsheet
- People who want an applicable lens design guide
- People that started lens design through other disciplines (such as mechanical engineering, physics)
- People who are self taught in optics to a certain degree (you can skip the math if you know it)
- People who are enthusiastic about lens design process, and can do trigonometry, I’ll try to make the math interesting.
Who this guide is NOT for
- People who want a quick fix to a specific optics problem
- People who just want a lens design solution, without the work that comes with it
- People who are physics-like researchers that want to derive theorems
- People who want the mathematical derivations
The goals of this guide with a spreadsheet
The goal is to use “classic” lens design by using tools in the modern era, such as a spreadsheet. “Classical Modern Lens Design”, which I do not think is an oxymoron.
I want to use lots of numerical results with real numbers, lots of diagrams, and lots of design methods. All in all, there about 50 tables, and over 50 images and diagrams.
Since our goal is to design with optics and not develop optics from scratch, equations will pop up when we need them. But the symbols and terms will be explained. For example, deriving Maxwell’s equations will not be covered here.
I think equations only are hard to follow, and ideally the equation complemented with examples are best.
I want to make this guide provided with real-world lens design with many practical examples to differentiate with optics books for academia or physics based optics textbooks.
And since I like a lot of stories, I’ll try to put in as many interesting stories pertaining to the topics that I can. I might go off topic if there is a fun story to be told.
I want to provide workable numbers clearly.
It will probably take you a while to read this guide, so I’ve attached a table of contents so you can follow along or pick up from last time. If you feel like reading the guide on a Kindle or iPad, you can download the PDF of the guide as well.

Get Your FREE Lens Design Guide with Spreadsheets
Enter your name and email for instant access to our Guide to Classic Lens Design (in PDF format) and the actual spreadsheets used in the guide!
??100% privacy, and we hate spam. When you sign up, we'll keep you updated usually with one email per week, occasionally up to a few times a week. Unsubscribe at any time.
Also, I have a BONUS of the EXACT spreadsheets that I use in this guide, so you can not only follow along with the guide step by step, but also use the spreadsheet for your own lens design.
Table of Contents
- Introduction to the general theme
- A brief history of classic lens design before computers
- The typical modern method for learning lens design
- Lens design forms we’ll explore with a spreadsheet
- Generalities of optical lens design
- Aplanatic lens design with a spreadsheet
- Anastigmat lens design with a spreadsheet
- Going forward
Who am I?
Hi, I’m Kats Ikeda, Ph. D, and my expertise is geometrical lens design, non-imaging lens design, and I’ve done a lot of product development based on optics and lens design. I love nerding out on optics and lens design talk.

What’s the job of an optical lens designer?
The job of an optical lens designer is to design the lens system, either by designing a lens or multiple lenses into a system. In actuality, a mechanical engineer or mechanical designer can also design a lens system with the knowledge of paraxial lens design. Here’s an overview of the optical lens design process, which can be broken down as follows:
- Derive the optical lens system and figure out a suitable focal length, back focus, aperture or F-number, field of view, and resolution for the system. In addition, ghost and flare, as well as the relative illumination should be worked out with systems that require them, and figure out the best lens system to achieve the performance needed. If it so happens that there are multiple systems, say two or three, that look promising, it’s usually a good idea to choose the one with lower cost, but we can proceed with two designs in parallel until the best system becomes clear in the later stages.
-
Once the system is derived, we choose the types of glass by considering the colour correction, Petzval sum, spherical aberration that we need. It’s often enough to calculate these in 1st order, or paraxial optics, so the calculations are relatively simple at this stage. This is where a spreadsheet can be extremely useful.
-
Correction of the 3rd order aberrations, such as spherical aberration, coma, astigmatism, field curvature, and distortion. Since there are higher order aberrations for many optical systems, the 3rd order aberrations are not set to zero, keeping these higher order aberrations in mind. Much of this is correction is done with lens bending, lens thickness, air thickness, and the index of refraction and Abbe number of the glass. Again, a spreadsheet can be used to calculate them.
-
Calculate the residual spherical aberration and the optical performance on the image plane by raytracing. Although correction of the 3rd order aberrations is a requirement, it is not the be all end all, therefore the balance of raytracing and the 3rd order aberration correction is important, thus requiring iterations for best results. If the system can’t be corrected, we take a closer look at the F-number and/or the field of view and we may have to change the lens system as needed.
In modern lens design, we go one step further, where once the raytracing results prove satisfactory, calculate the spot diagram and the optical transfer function (OTF) to get usable numbers for the evaluation of the lens system, and move to prototyping the lens.
The lens systems that we will explore here will be enough to calculate the 3rd order aberrations. Of course, there are systems like wide angle lenses that cannot be satisfied by only 3rd order aberration correction.
Now this overview doesn’t include laser optics, or illuminations optics, and physical optics and many others, but for classical lens design, it is a good rule of thumb to go with 3rd order aberrations and a spreadsheet.
A brief history of classic lens design, before computers
How did the people in the past design a lens, before computers came into the lens design picture?
In 1812, Wollaston’s Periscope was the first documented lens that considered optical performance. At that time, there was no such thing as optical lens design, so the shape of the lens was most likely done experimentally by trial and error. Lens fabrication requires a high level of precision, and also a high level of metrology. In order to avoid this painstaking process of lens fabrication and measurement, a method for doing the same thing on paper was devised, thus giving birth to ray tracing and lens design. Obviously, writing the calculations down on paper doesn’t have variability like in manufacturing, and raytracing can provide even minute differences in performance to be quantified right in front of us. The possibility of precise calculations became a job on its own, and produced many high performance lenses over time. At the same time, lens designers were required to do complex calculations and work around them.
Coffee break: some historic lens designers
I recently bought A. E. Conrady’s book, Applied Optics and Optical Design, parts one and two. Part one was published in 1929, but part two was not finished until 1960.
His daughter Hilda G. Conrady Kingslake finished her father’s book with the help of one of his best students, Rudolf Kingslake. I didn’t know Conrady’s daughter was prominent in optics herself, and was married to Kingslake. They both lived to be 100. I sometimes wonder what kind of conversations that they might have had.
The typical modern method for learning lens design
The current lens design learning curve
I think there are a few ways to learn lens design in the modern age, with all the tools we have today.
- Learn the optics theory in class, and how to use the software such as Zemax/Code V/Oslo in an Optical Science University.
How many high level schools are there in the world? Some in the US, some in Germany, perhaps. You need a good study program to learn at a high level. -
On-the-job training in an optical company or related field.
Maybe you have a mentor, or coworkers you can learn from. You can also learn by going into the deep end, doing real work. -
You’re learning on your own through books, and software.
Maybe you bought a book or two. Maybe you downloaded free (or paid for) lens design software. Maybe you took an online course in optical lens design.
I’m sure that most lens designers are some form of the three. I believe that the crux is expensive proprietary software.
My brief lens design story
I was first exposed to optics from classes in Physics in high school, but really started taking an interest into it when I started photography as a hobby. I learned more about lenses and their history. There was a whole world of science that seemed very simple on the surface compared to quantum physics or string theory, but was truly a science onto its own, with applications far beyond what I could image at the time.
There are a number of books that I really enjoyed reading and implementing (Kingslake, Berek, Conrady), but the best books are very classic in nature and difficult to implement, and therefore difficult to appreciate for me at the time.
Textbooks are great due to the wealth of knowledge, but they are tough at the same time. Lens design Fundamentals (Rudolf Kingslake), Applied Optics and Optical Design Part 1 and Part 2 (A. E. Conrady), Modern Lens Design (Warren J. Smith), and Optical system design (Robert Fischer), Introduction to Lens Design: With Practical Zemax Examples (Joseph Geary), are all great books, just to name a few. But I feel textbooks, in general, are difficult to follow for the novice, especially without previous knowledge. The more I read these books, the more I felt that these textbooks were written for the author and not the audience, and routinely got frustrated as I got lost and could not follow the concepts.
In my opinion, on-the-job training is the best way to learn, there’s more at stake, and you’re getting paid, after all.
Action Step: Identify where you stand in the lens design learning curve. Have you gotten on-the-job training? Are you self-taught? Were you lucky enough to learn lens design in class?
The lens design labyrinth and how a spreadsheet can help
So what do we do when we are thrust with a lens design task? I think most of us dive into the software. Zemax, Code V, Oslo. For practical examples, the Zemax manual, the knowledge base for Zemax and the Zemax forum community are all great, and if you are searching for a specific topic that’s fine, but the novice may not know what they should start learning, and these examples are hardly systematic.
In the modern era, the computational power of computers has become extremely high, and with that, lens design has changed. It is possible to calculate complex results in a very short amount of time, so the technical aspects have improved tremendously.
What hasn’t changed is the fact that lens design is still performed with some degree of trial and error. As long as trial and error exists in the process, there remains multiple paths towards the answer to a problem. In fact, even though theoretically sound arguments and optimization of our workload is paramount today, there are many lens designers that still use “experience” and/or “educated guesses” when designing a lens.
However, for lens design to become a technology worth pursuing, a “good” lens design cannot be a result of one person’s lucky guess that can’t be explained. The concepts have to able to be explained and replicated by others.
Not exclusive to lens design, any endeavor that can be described in part with word “design” has some degree of freedom. The designer takes the degree of freedom handed to them, and within that scope, have to make many decisions based on whether or not those decisions lead to a better design or not. In general, this requires quite a bit of experience, and oftentimes even designers equipped with experience can have a difficult time figuring out what is best for a particular design. Each designer, at each point in time, makes decisions based on their own knowledge, and the trial and error method ensues.
Facing this reality, I think there are two things that need to be accomplished so that lens design can become a study worth applying. One, the lens designer must be able to systemize their process on why and how a particular lens was designed that way. And two, since lens design requires many difficult design decisions, there is a great benefit in knowing the theory to the process. There are a lot of documents on lens design but very few with the scope of presenting the theory with the usefulness in mind.
To describe lens design with a metaphor, it’s like going through a wooded valley blindfolded, with earplugs, with a huge backpack, and only a stick to see how far you’ve gone down in altitude. We, as lens designers have to find the lowest point in that valley.

There are two ways to make this journey feasible.
1. Use a tool to systematically check the performance of the optical system to the performance goal, such as geometrical optics.
2. Use some method to structure the lens design process so that it can be followed, and the process is built on top of it, like aberration theory.
The grand scheme of the history of lens design follows this trend. But I think that in the modern computing era, the advancements have become so large that the very beginnings of the methods are either lost, not applicable, or too primitive at first glance for people to adopt.
Lens design without expensive proprietary software
That’s why this Spreadsheet Design Method concentrates on Gaussian optics and 3rd order aberration theory.
Optical lens design requires the complicated balancing of several aberrations between several surfaces, so understanding the optical system is extremely important. Also, by using Gaussian optics and raytracing through a spreadsheet, I want to evaluate as many optical systems I can by looking at real-world lens designs as references.
So what are the benefits of mastering “classic”, or “low-end” lens design, with the help of a spreadsheet?
Learning high-end lens design starts with mastering low-end lens design. But applying textbook material without the optical design software is difficult. On the other hand, just diving into learning the software can cause a disconnect in the optics theory and the lens design process. I see it all the time. You get really good at using the software, without learning the underlying theory.
Our goal is to break down the function of optical design software with a spreadsheet.
Software examples: Zemax, Code V, Oslo
- each one is good at different things, but all are rooted in raytracing
- some things can’t be done by hand
- problem is you can become an expert in handling the software, but not in lens design itself
The pitfalls of automatic lens design
Computing and Automatic lens design is a powerful tool, but has some problems that need human intervention.
- No singular solution: we need parameters, weight, time
- May not get the best solution, like a local minimum
- Tolerancing while optimizing (sometimes possible with multi configurations)
- Can do optically meaningless optimization if merit function minimizes itself
- Only makes merit function small
- Cannot change large factors: choosing correct glass, splitting lenses
- Ill conditions: trying to find solution where there are none, such as two conflicting parameters
Action step: If you’ve used lens design software before, think about how many times you may have press a button not knowing its function, in order to optimize a lens. Did you think about the lens design process?
Lens design forms we’ll explore with spreadsheets
With all of that said, let’s take a step-by-step approach on which optical systems to explore.
A single lens objective
A single lens, or singlet, is a one-lens system. This guide will provide a little explanation, some history and some real-world examples. We’ll look at what aberrations we need to correct for different applications, and how those aberrations change with the shape of the lens.
Achromatic doublet
The achromatic doublet is a useful lens system because it corrects chromatic aberrations. Actually, we see the doublet in multi-lens systems if we break them down. The important parameters for an achromatic doublet are chromatic aberration, spherical aberration, and Coma, so we will explore them in detail with real-world examples.
Cooke triplet lens
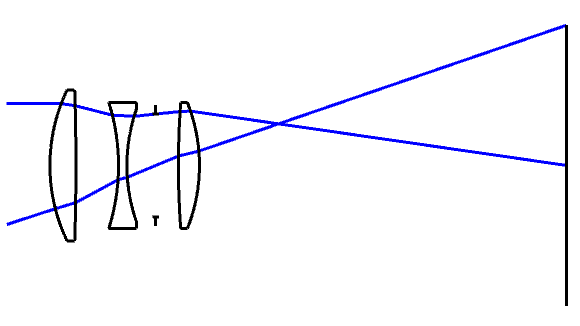
Perhaps the most famous and ground-breaking three lens system. In addition to aberrations such as spherical aberration and Coma, an Anastigmat like the Cooke triplet includes additional aberrations of Astigmatism, Distortion, and Lateral colour. Finally, as above, we’ll look at some real-world examples.

Since this is the electronic age, a lot of lens design includes Thin films, Illumination, Optical fibers, Lasers, Physical optics, not just imaging for cameras, like before.
I want to classify lens design into various forms:
- Classic lens design: Geometrical optics, Aberration theory, Lenses, Prisms…
- Modern lens design: Gaussian beams, Thin films, Colour theory, Physical optics, Wave optics, Diffractive Optics, Fourier optics… (Classic optics are mainly lens design for cameras, and modern optics are for more modern systems, that usually use semiconductors such as CD/DVD/Blu-ray, LCDs, Astro lenses, stepper lenses, Laser Cutting Machines)
Other lens design forms that are interesting but NOT covered here are:
- More complex design forms such as Double Gauss, Sonnar, Retrofocus, Telephoto, and other lens design forms
- Aspherical lenses
- Zoom systems, afocal systems anamorphic systems
- Illumination systems
- Wave optics and/or Physical optics
- Thin Films
- Laser systems
Generalities of optical lens design
How to express the system
Express the optical system
Before performing any lens design, we need to express the optical system with numbers. That means math.

Without the math, it is very difficult to go forward, because we can’t set up the system, and we can’t do any real design as well. The giants of lens design, from 100 years ago could be better described as mathematicians than optical scientists, and were all masters of math. I will try to make it as interesting as I can, or make sure that it is unobtrusive and usable as possible.
For reference, here are the “positive” and “negative” values I will refer to, depicted in one of my most trusted books, Field Guide to Geometrical Optics, by John Greivenkamp.
Be careful, some books, schools, optics companies, and countries use different axes and coordinates.
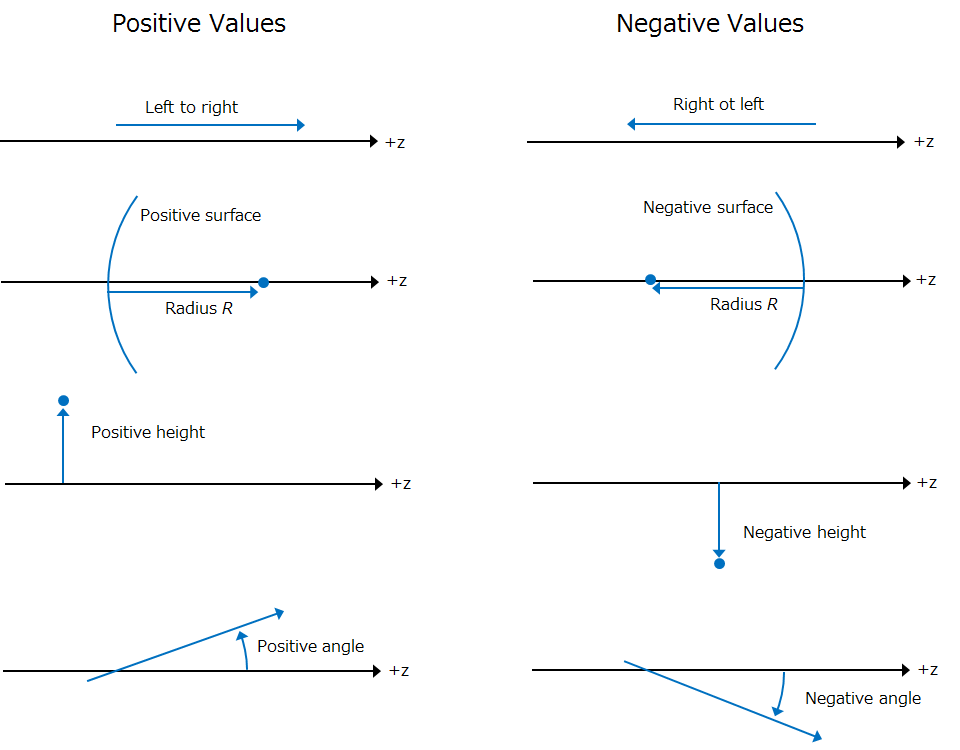
The axis of symmetry of a rotationally symmetric optical system is the optical axis, and is the z axis.
All distances are in Cartesian coordinates. Above and to the right are positive; below and to the left are negative.
All angles are measured in the Cartesian sense as well. Counter clockwise angles are positive; clockwise angles are negative.
The radius of curvature of a surface is defined to be the directed distance from its vertex to its center of curvature.
Light travels from left to right (from –z to +z) in a medium with positive index of refraction.
Although I won’t get into reflection at all in this guide, the signs of all indices of refraction following a reflection are reversed.
Let’s draw a simple lens system
First of all, I’d like for us to try to draw a few lenses so we can express them visually. I’m going to use graph paper, a ruler, compass, and draw it out. Yes, even in the digital age we live in, I’d like to try this.
Spreadsheets break down the lens into components, and drawing the lens is the same, conceptually.
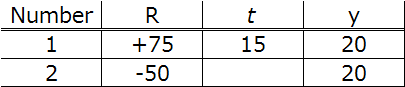
Radius R, distance on axis t, ray height y
So let’s check out the table below. We have a positive lens, so let’s try to draw this lens. We’ll assume all of the lenses are circularly symmetric, so we can make do with the cross sectional view of the lens.
First, we’ll draw the optical axis. Easy enough. Circularly symmetric means the lens doesn’t change in shape when we rotate the diagram along this optical axis.
The entrance ray goes from left to right. (You can do it whatever way you like, but I’ll go with what I’m comfortable with, and I’ll be consistent with it. Sometimes going along with textbooks can be easy, and not tedious)
The positive lens we want to draw has two refractive surfaces, and we’ll name them surface 1 on the left, and surface 2 on the right. So we’ll denote the radius of curvature, the thickness, and ray height as such. (R1, R2, t, y1, y2)
Step two, take a location on the optical axis and set it as the vertex of the lens by drawing a dot. We’ll call this point V1.
Step three, we’ll draw the refractive surface of the first surface, denoted as R1, for radius. The first radius is a positive number, we’ll take the center of the lens on the right side of the optical axis and draw it with a compass.
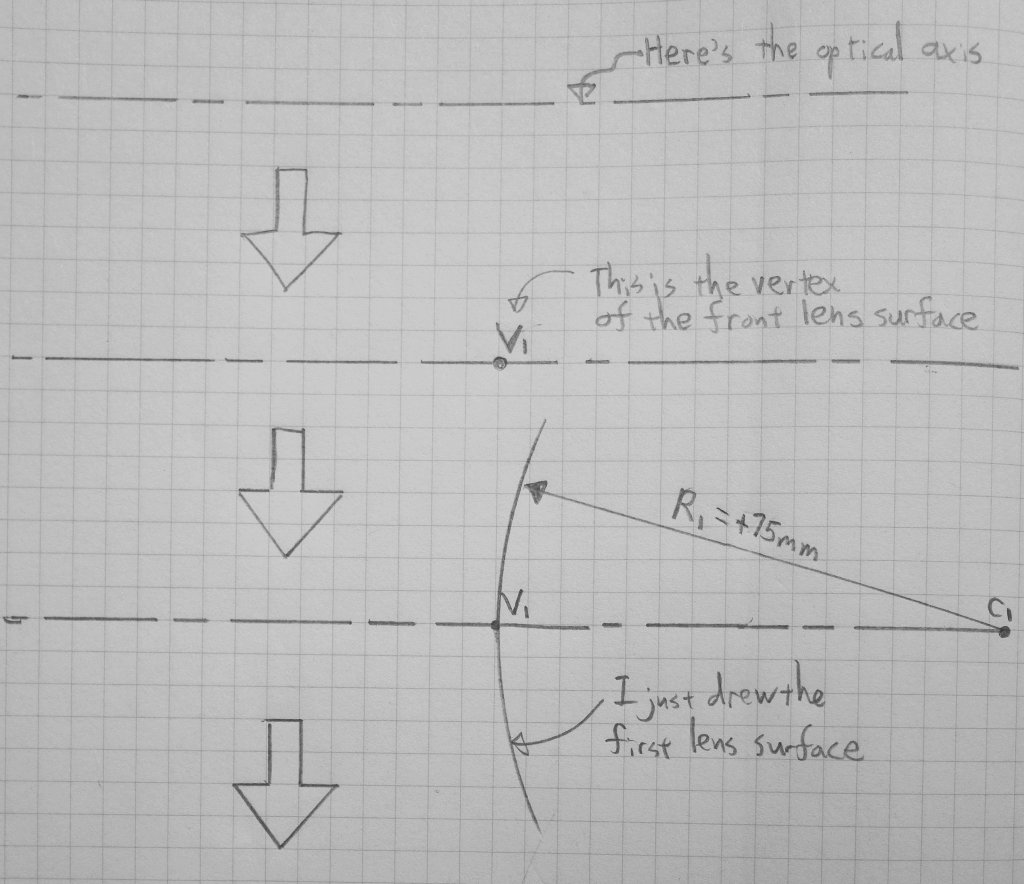
Since y is 20mm, the diameter of the lens is 40mm.
The next vertex V2 is drawn at 15mm to the right of V1. Thus the distance between the two apexes becomes the thickness of this lens, denoted by t, and equal to 15mm in this case. Let’s draw this surface as well. It’s convenient to think about each surface with its own coordinates, for example the first surface has its (0,0,0) coordinate at the vertex V1, and likewise for the second surface, its coordinate (0,0,0) is at the vertex V2. This comes in handy when we ray trace, since the coordinates become relative to the surfaces where refraction occurs.
Going forward, the next step is taking the point 50mm from V1 and drawing the surface from there, again, with a compass.
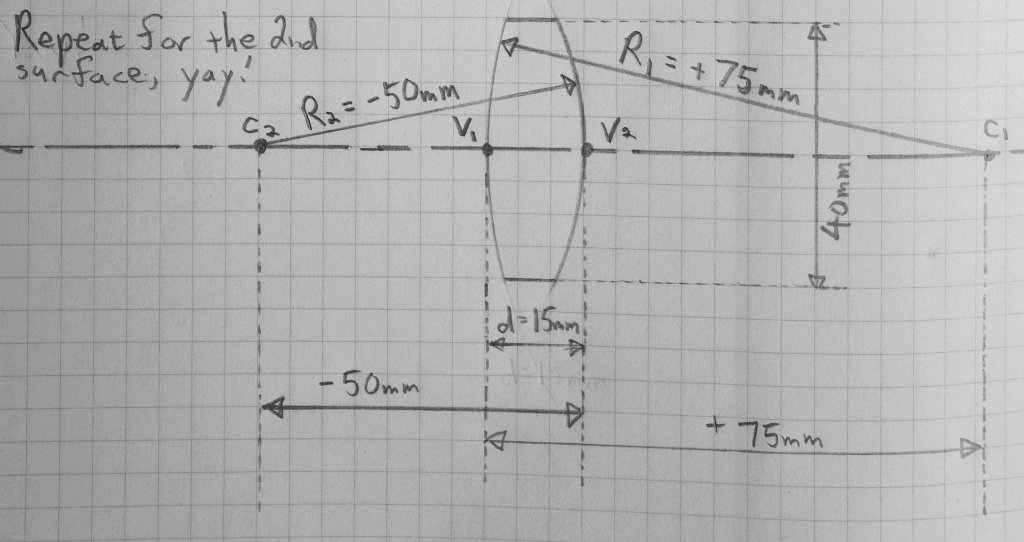
(whoops, looks like I wrote “d” for the lens thickness instead of “t” like I have above. But you get the picture)
There we go, the lens is drawn, that was a lot of work for a simple positive lens, which we take for granted. There were enough terms and order in there that we have to learn and utilize in order to be able to draw this.
I’ll let you in on a little secret; I’ve played around with this “drawing a lens” idea for fun with a lot of colleagues when I get a chance. A surprising number of people have a hard time figuring it out and make simple mistakes. A lot of camera books and lens books sometimes explain the history of Double Gauss lenses and other lens forms. Reading surface level material compared to actually moving your pencil and doing things can make all the difference in becoming an expert lens designer.
Action step:
Draw a lens from scratch, preferably by hand, with the method above Trust me, this will help with visualization.
Terms and symbols
As I have in the table below, there are a lot of terms that come up often in lens design expression.

n = index of refraction
If you don’t have access to a glass catalog, I’d suggest you get one so you can look at it and refer to it when needed.
Links to charts(PDF):
Schott glassmap PDF
HOYA glass map PDF
Interactive glass maps:
Schott interactive glass map
HOYA interactive glass map
Datasheets:
Schott datasheet
I have a nice laminated poster that a HOYA employee was handing out one time I was passing by their booth at a conference trade show for free.
Since we’re not doing extremely precise physics, we can approximate the index of refraction of air to be 1.00. Usually we use about the 5th digit in spreadsheet calculations.
\(\lambda\) = wavelength
This is the wavelength of the light. As in the table below the primary wavelengths of a mercury lamp are used in calculations. We usually use subscripts for the denotation and use nd, for example.
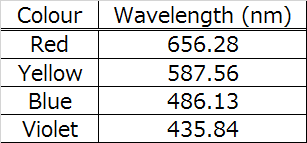
For camera lenses, the d line or the e line are used. The d line is for Na(sodium), and we see this often in experiments in Physics. The C line is red, and the F line is blue. When we eventually draw the aberration diagrams, it is convenient to use colours that correspond to their wavelength colours.
In the photopic range, the eye has its highest sensitivity around the d line, so it is used often (The actual photopic peak is about 550nm).
When we are dealing with binoculars and other visual optical systems, the C line to F line is sufficient, and with camera lenses the g to C lines are used for colour correction. Particularly important is the violet wavelength g, since the early days of black and white film, the sensitivity of the film was shifted to shorter wavelength, and the performance at 435.84nm was required because that was the range that the film emulsion reacted to light at the time. Therefore, for a long time, the wavelength for violet, g, was used routinely in the calculations.
Fast forward to the modern era, in digital cameras it is sometimes required to account for near infrared light depending on the application, as semiconductor sensors can react to longer wavelengths.
\(\nu\)
\(\nu\) = Abbe number
There was a famous mathematician Ernst Abbe that established this term, and it denotes the dispersion of the glass. If you shine white light into a prism, we can see a rainbow, and we can see the rainbow from violet to red, namely the g to C lines.
When Isaac Newton saw this, there weren’t many different glass types at the time, so he didn’t know that there were different dispersion depending on the type of glass. After seeing the rainbow made by the prism, he concluded that he could not make a high performance telescope by using refractive lenses since it would cause too much chromatic aberration, and opted to develop a refractive telescope. Thus to this day, a telescope named a Newtonian telescope is one that uses reflections with mirror lenses rather than refractive lenses.
Abbe’s theorem is as follows:
\[\nu_d = (n_d – 1)/(n_F – n_C)\]
so if the Abbe number is larger, there is less dispersion, making it a confusing term in an intuitive sense, but it is what we have to live with.
Flints and crowns
Here’s a picture of an optical glass map.
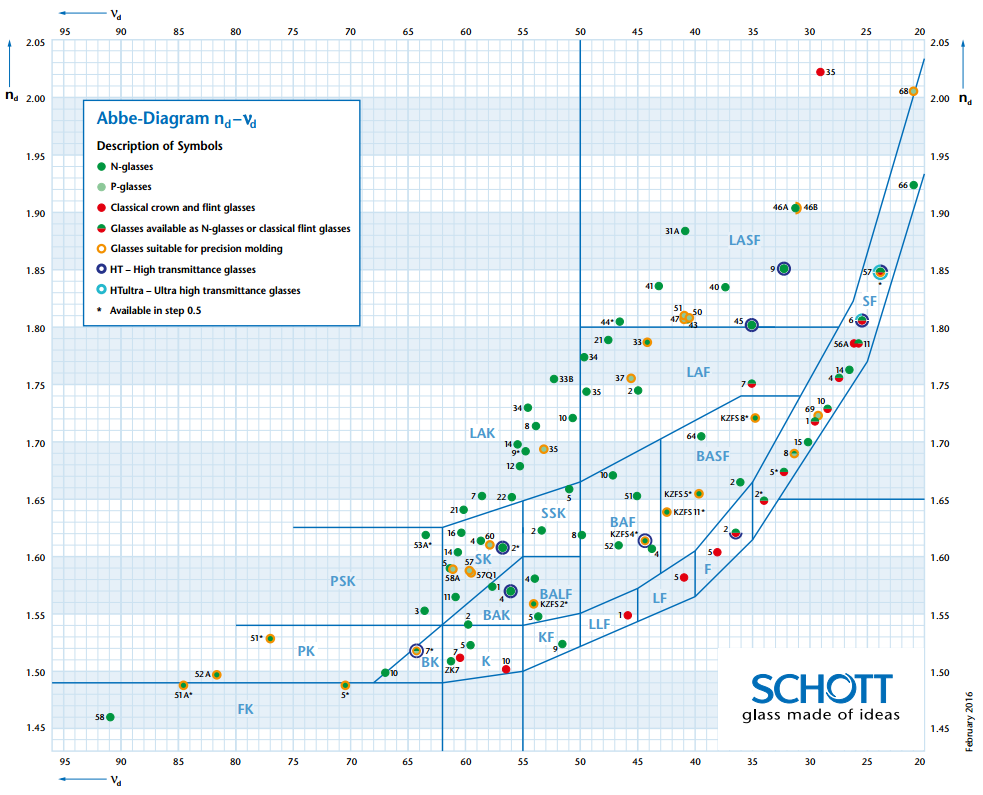
There are all kinds of symbols used to express the glass. Some examples are BK7, K3, F2, which you may have heard of. The letter is the group of glass, and the number is used to further segment glass types.
First of all, we can make the distinction between flint lenses crown lenses. Crowns have small dispersion (large Abbe number), and flints have large dispersion (small Abbe number). BK, K are representative of crown glass, and F is representative of flint glass.
For example, for telescope objective lenses, a positive crown lens and a negative flint lens are used.
Some other commonly used glass types are SK and SF lenses, which are crown glass with a high index of refraction, and flint glass with higher dispersion, respectively. Crown glass are mostly silicon, or sand, and SF had lead in them, which has changed since we are removing lead from most things lately.
After World War II, development of Lanthanum and tantalum lenses began, and were relatively expensive due to the difficulties in manufacture. These types of new glass made it possible to make 50x zoom lenses for television lenses, and high performance 50mm F1.4 lenses. The refractive index of these lenses are much higher, and we can reduce the about of aberration since the radius of curvature can be kept that much smaller.
Rays and raytracing
Cartesian coordinates and surface numbers
I like using the z axis as the path of light, so left to right is the positive direction. This is a more modern way of expressing the optical system, so sometimes in old books you may see different coordinate systems. Just as a reference, more traditionally, the path of light was taken as the x coordinate, not z.
And perhaps to no surprise, I will use surface 1 as the leftmost surface, and count 1, 2, 3… from there. I’ll use k for the final surface.
I also use the y axis as up and down, up being positive.
This is perhaps used commonly today, but some books have different coordinate systems, so it’s always a good idea to check. Also, depending on who you’re talking to, like machining people or systems people, they can have different coordinate systems, so again, it’s always good to check.
Ray terms
Rays are in 2D for now, and we’ll name some terms that we will use for raytracing later.
Paraxial systems
Paraxial raytracing is for tracing the rays are close to the optical axis, thereby simplifying the system with the following approximations:
\[\sin{u} = \tan{u} = u\\
\cos{u} = 1\]
In the paraxial system, there are no aberrations and an object at one point only has an image at one point. This aberration-free concept is usually referred to as Gaussian optics, and really helps when using a spreadsheet. I keep my Field Guide to Geometrical Optics handy to reference the raytrace equations.
Gaussian optics: thin lens
Thin lenses are systems with the assumption that the thickness of the lenses are zero. I understand it’s hard to imagine a lens with two positive surfaces without a thickness, but think of it as a surface that bends light.
In paraxial systems, the thickness of a lens is zero, and for optics such as telescope objectives (which we’ll get into later) the focal length is much larger than the lens thickness, so initial calculations can be done easily as thin lenses, and we can add the thickness of the lens and do additional calculations afterwards.
Even triplets (again, which we will look into later) are initially calculated with three thin lenses, and then made thick afterwards. If we use thick lens equations for everything, some calculations become needlessly complicated.
With thin lenses, many simple calculations can be made, and it is easier to look at the optical design as a whole.
Gaussian optics: thick lenses and principal planes
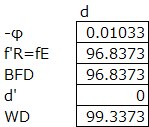
There are focal planes in a lens, the front focal plane and the rear focal plane. A parallel beam passing through a lens has a focal point where the rays focus to one point. This is called a pencil of rays (which I chose for this website’s name).
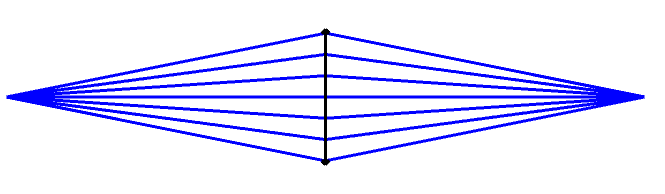
The backfocus of a lens is easy to understand, as it is the length from the rear surface to the focal point, but the focal length is a little harder to grasp for people seeing the concept for the first time. As experts in lens design, when we speak to people that aren’t experts, we need to keep in mind that many people can confuse the back focal length to the focal length. To keep this in mind is a simple act of kindness.
Ray tracing method and YNU ray tracing
Since I’m using the coordinate system mentioned previously, forward raytracing will follow these two equations:
$$
n’u’ = nu-y\phi\ \\
y’ = y+u’t’
$$
That is, the ray is going from left to right, in the positive direction.
Some terms we usually see are Scaled thickness: \(\tau = t / n\) Power of the surface: \(\phi = (n_2 – n_1) / R\) Scaled angle: \(n_u\)
There is also the reverse ray trace, with the following equations:
$$
nu = n’u’+y\phi\ \\
y = y’-u’t’
$$
This is the ray is going in the negative direction.
As mentioned before, there are a few ways to represent the raytrace depending on what coordinate system we use, and what sign convention we use. I use the sign conventions in Field Guide to Geometrical Optics.
Some associated equations for raytracing are
$$
nu_2 = nu’_1\ \\
y_2 = y_1 + \tau nu_2
$$
A comprehensive site on raytracing is from the optical component vendor website Edmund Optics’ paraxial raytrace equations.
Another great resource is the YNU ray trace worksheet by Chris Berger. If you want to check your raytrace calculations, this is the place to go, there are a lot of great optics calculations on this website.
Nowadays, computers are so fast that these calculations are easy once they are set up. I think there is a place to figure out what the equations are doing, so that we can look back to our lens design software and better understand what is going on under the hood. It’s amazing to imagine people used to do this by hand, abacus or not.
Let’s try this YNU raytracing with a calculator, set it up in a spreadsheet.
To use the sheet, you set up the spreadsheet so that it does these calculations for you automatically, and sequentially.
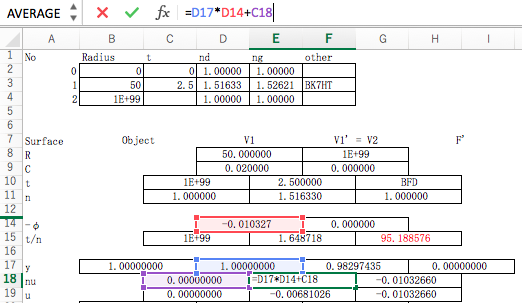
So let’s work out a few examples with this raytracing tool. This is where things get fun.
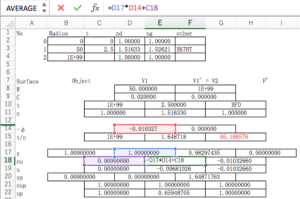
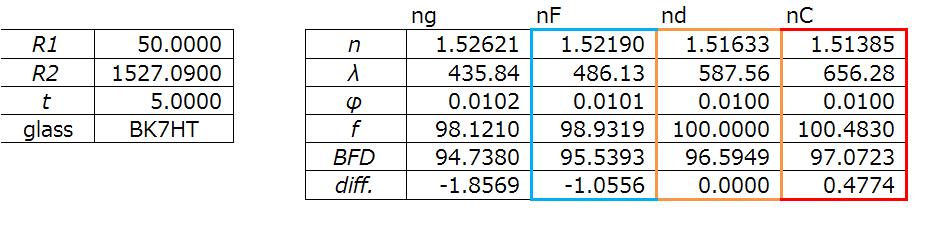
I’m going to take a lens with the material BKHT at the d line. The index of refraction is 1.51633. If the radius of curvature of the front surface is 50mm, it will look like this:
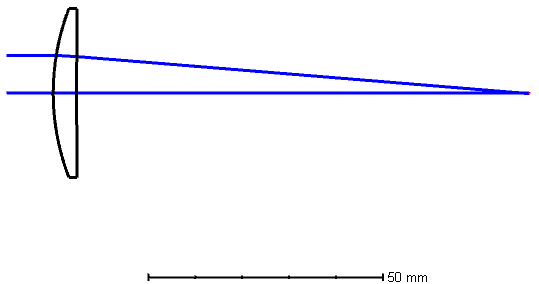
Let’s set up the paraxial raytrace table and figure out the numbers. Notice that I will use y1=1, and u1=0 for the pilot ray.

The back focal length, lens power, etc are also calculated.
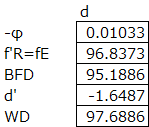
We can also do the same calculation for this lens flipped around.
Let’s set up the paraxial raytrace table again, again using y1=1, and u1=0 for the pilot ray.
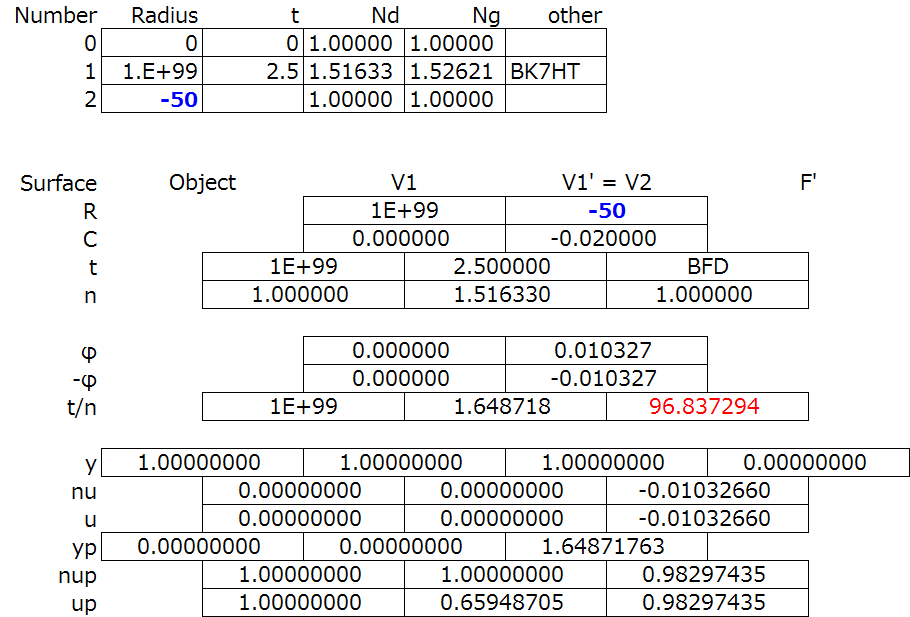
These are actual lens design examples, and you can now see the amount of information that you can calculate from a simple lens.
Action Step:
Take your favourite spreadsheet program, such as Excel / Google Sheets / Numbers and do the calculations for this lens.
Some lens types and their principal planes
The principal points (also looped in as cardinal points) of the makes the lens apparently have crossed the principal points, and the lens can be treated as if all of the refraction happened at the principal planes, therefore the focal length of the system can be determined.
The principal points can also be used to find the magnification of the system, since it is the distance of the object and image from the front and rear principal points.
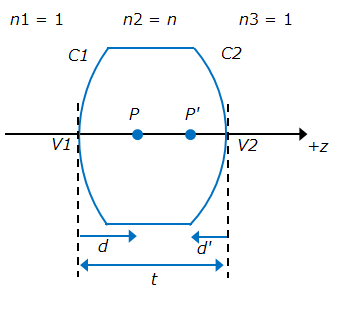
As I’ve referenced many times, I use the thick lens equations in Field Guide to Geometrical Optics. If you haven’t noticed, I really like this book, it’s the perfect size to carry around for reference.
The equations for the calculations used here are
$$
\phi = (n-1) [C_1 – C_2 + C_1 C_2 t (n-1)/n] \\
f = 1/\phi \\
BFD = f (1-C_1 \times n-1)/n) \\
FFD = -f (1+C_2 \times (n-1)/n) \\
d = BFD – f \\
d’ = FFD + f\\
$$
Where (\phi) is the lens power, BFD is the back focal distance, FFD is the front focal distance, d is the front principal plane distance from the front vertex, d’ is the rear principal plane distance from the back vertex of the lens. n is the index of refraction, (C = 1/R) is the lens curvature, t is the lens thickness.
I realize that most of you reading this has a concept of lens power, but I want to take the time here to point out that thinking in terms of curvature is really useful in lens design, especially when dealing with aberrations and tolerances. However, at the same time, in a diagram it is much easier to visualize a lens when it is written in radius rather than curvature, due to its much familiar units. Oh the irony!
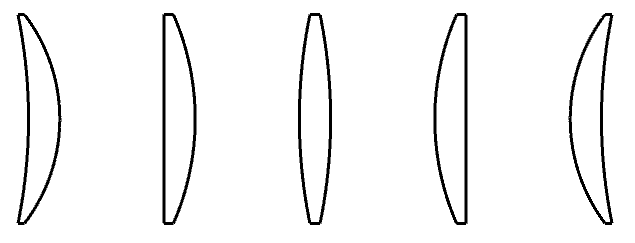
Here’s a list of some common single lenses that we use often in lens design. To keep the principal points (and planes) in mind when setting the system up is a good idea so we can get the performance we want.
Spreadsheet calculation of principal planes for a double convex lens and a plano-convex lens are below.
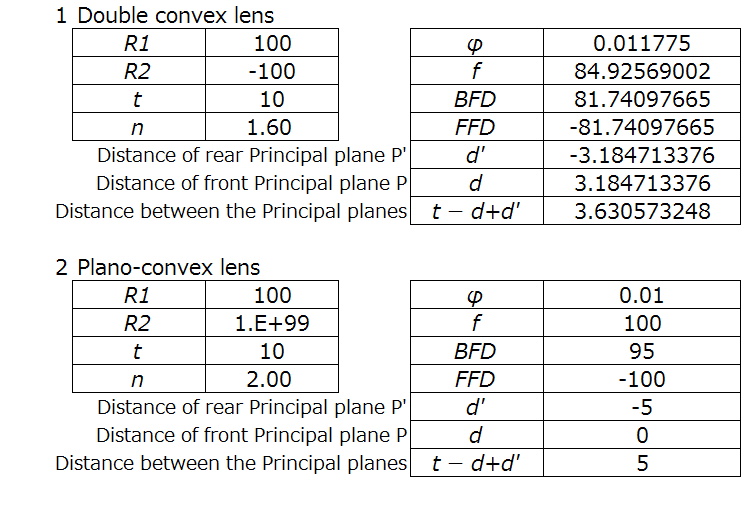
We can see that for a double convex lens, the principal planes are mirror images of each other and symmetric. For a plano-convex lens, the principal planes are identical to a thin lens.
Spreadsheet calculation for two different meniscus lenses are below.
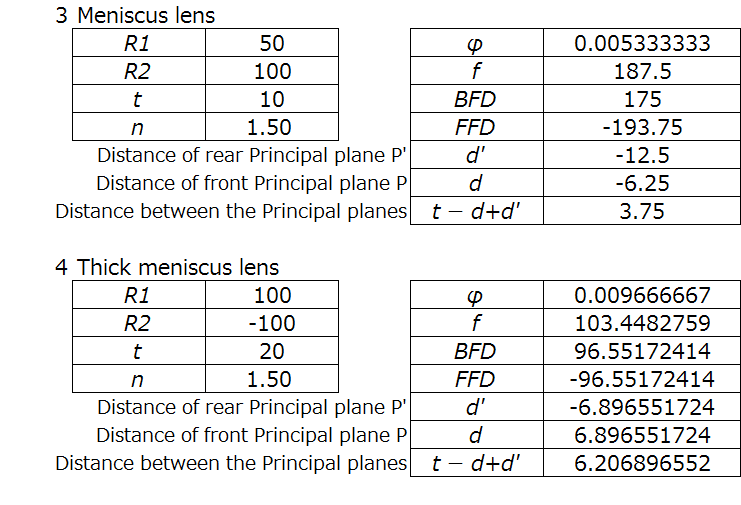
We can see that for a meniscus lens, the principal planes shoot out to the front of the lens. For a thicker meniscus lens the principal planes shoot out even further to the front, and the distance between the two planes is further as well.
Spreadsheet calculation for a a concentric lens is shown below.

A concentric lens has principal planes on each of their surfaces, and appear like thin lenses. If we place concentric lenses in succession, we can place principal points of a thick lens in one location. As an aside, spherical ball lenses are a type of concentric lens.
Spreadsheet calculation for a a null lens is shown below.

Null lenses are usually used in metrology, and the Petzval sum (and therefore the field curvature) is zero, even though it is a thick positive lens. We’ll get into Petzval sum in later chapters.
The six examples above are single lenses, but we use them throughout our lens design process, deciding which lens to use when, in each situation. The conceptual knowledge of principal planes for each lens type is important when setting up our optical system.
Action step:
Calculate the principal planes of these lenses, and draw them on a sheet of paper. No drawings from me as a reference this time, you’re on your own 😉
For a lens system, you can ask yourself, “where do we want the principal points to be?” This is a great way to think about the system, because it depends on the lens system that we are designing.
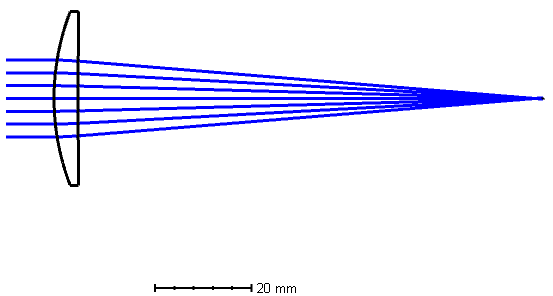
Telescope objectives
Let’s take a look at two very common doublets for telescope objectives, the cemented doublet and the separated doublet lens.
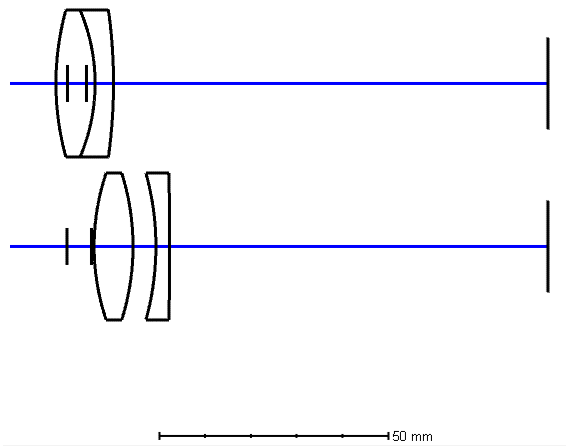
For the images, I am using the optical design software Zemax , but i haven’t found a good illustration software that handles the drawing of lenses well. I’ve done them by hand in the past to get a feel for the drawing process, but even drawing them in graphical software can be beneficial.
Looking at these lenses closely, you can tell that for the split doublet, the principal points are on the left of the lenses, so the same focal length gives you a lens system with a shorter total track length. (Also, we’ll get into this later but the spherical aberration can be made smaller so the F-number can be made faster as well)
Three types of camera lenses and their principal points
There are three types of camera lenses that I want to showcase here, the Double Gauss type, the retro focus type, and the telephoto type.
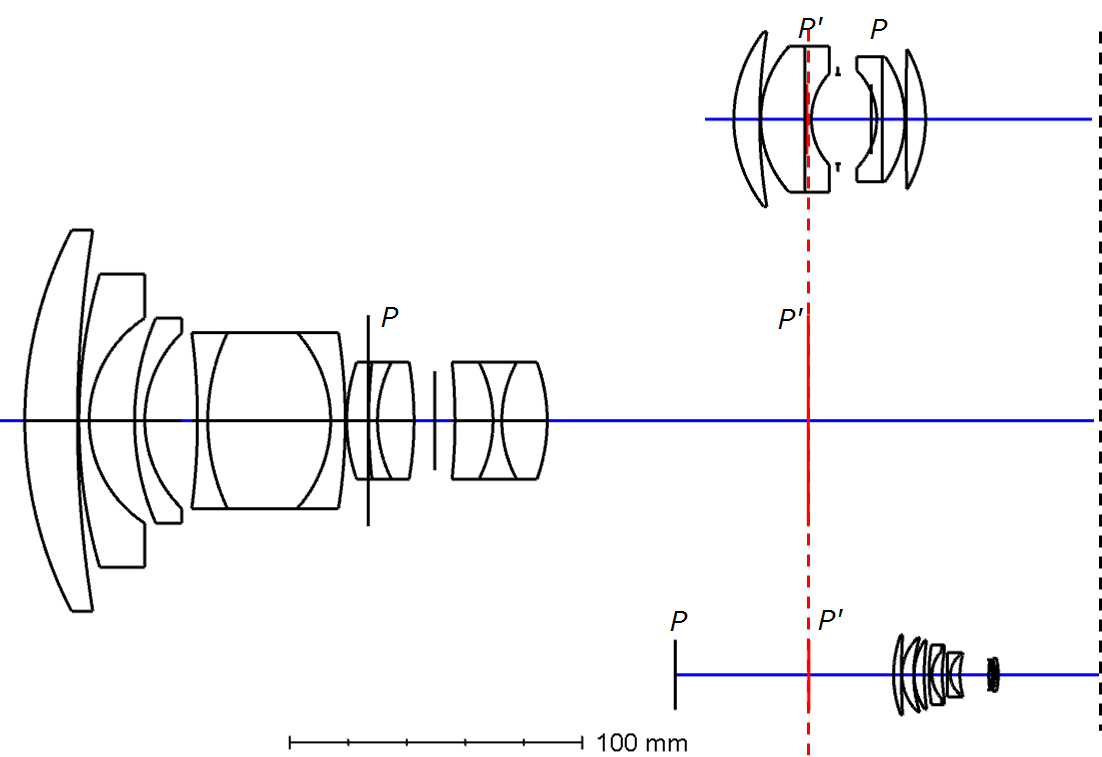
If you noticed, I’ve scaled the images all to 100mm focal length. You can tell because the red dotted line lines up with each other, which is where the rear principal plane is located.
The double gauss lens look the most “normal”, and the focal length is inside the lens, and look to be about symmetric.
The retrofocus lens has a negative lens group at the front, and a positive lens group at the rear, and the back focal length can be made long. We can see that the total length of the lens is also long compared to the focal length. The above diagram looks large because it is scaled, but retrofocus lenses are usually relatively short in focal length, so the actual length of the lens is not extremely long. We see this a lot for shorter focal length lenses for DSLR cameras (i.e., it has a mirror).
The telephoto lens is the opposite of a retrofocus lens, as it has a very long focal length but the actual length of the lens is relatively short (compared to the focal length). This is achieved by a positive lens group in the front, and a negative lens group in the rear. This makes the lens smaller in size, and therefore lighter, while the focal length is long.
As we can see, the optical concepts of these lenses are very clear just by looking at their principal planes. What’s more interesting to me are that the reasons for the optical concepts all have actual real-world use in mind. Here’s some lens data if you’re interested.
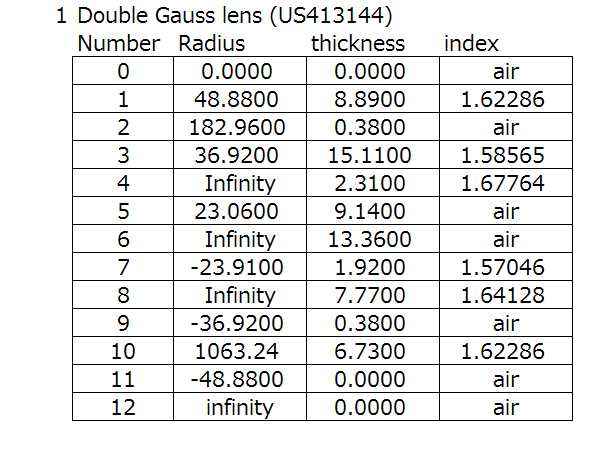
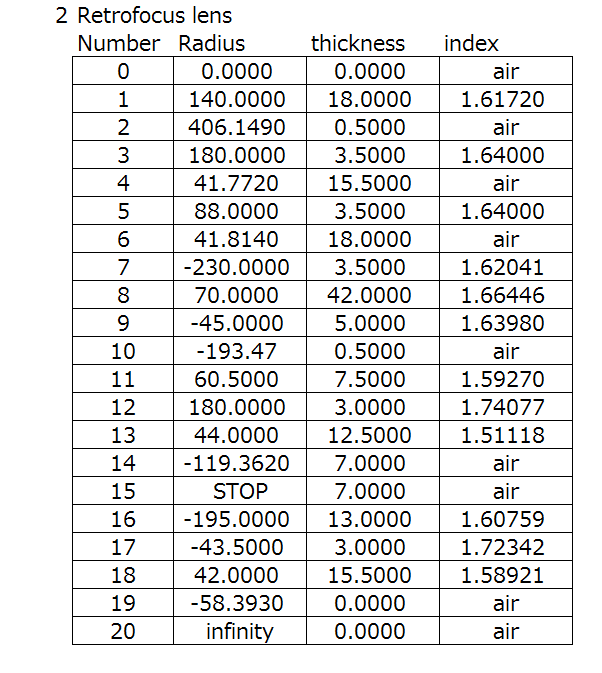
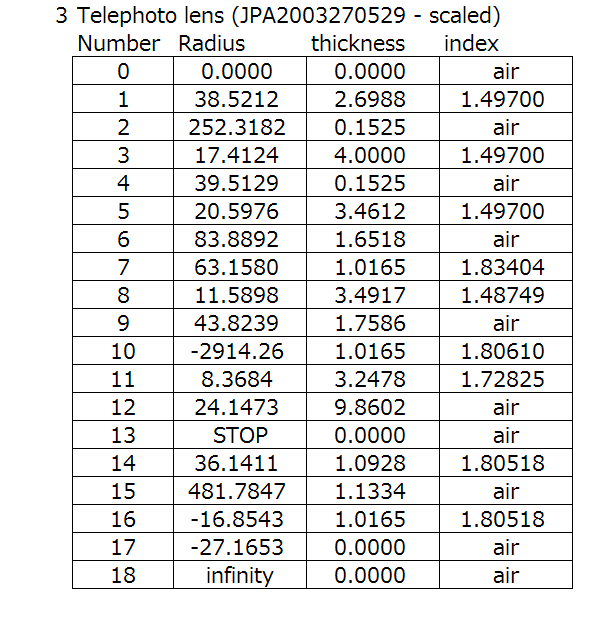
Action Step:
Pick a lens of your choosing (a patent design, your own design, a design in a textbook, etc.), draw it out, and write out the principal points after calculation.
By the way, I’m not totally against proprietary ray tracing and lens design programs. They are very good at doing complex calculations very quickly. Hey, I’m using Zemax for these lens diagrams.
A higher level of lens design and raytracing is possible with above with a more complete program, which is possible with coding. There will be several subroutines that need to be made, so it’s easier said than done, but if you have the ability to code, it may be a fun experiment to do. I guarantee that you will know how the proprietary programs work, although it will probably take a lot of time to perfect. My goal is for all of us to be able to understand the raytracing behind the software.
I liken it to a car. It’s relatively easy to drive a car, while it isn’t as easy to build one. It costs some money, but buying a car will give you the ability to go farther than you ever could without it.
Aplanatic lens design
The seven deadly aberrations

By Hieronymus Bosch – “The Seven Deadly Sins and the Four Last Things”, painting by “Hieronymus Bosch”, Public Domain, Link
Compared to the seven deadly sins (pride, greed, lust, envy, gluttony, wrath, and sloth), the seven aberrations are more straightforward to correct (your mileage may vary).
The seven aberrations are:
- Axial or longitudinal chromatic aberration
- Lateral or transverse chromatic aberration
- Spherical aberration
- Coma
- Astigmatism
- Field curvature
- Distortion
The first two are 1st order aberrations while the other five are monochromatic 3rd order Seidel aberrations.
For camera type lenses, there are aberrations that need to be corrected in order to get an image with high performance. Some textbooks mention piston and tilt, but are not actually true optical aberrations, as they do not represent or model curvature in the wavefront, so we won’t get into them any further here.
Also, there are higher order of aberrations that need to be corrected for high performance lenses, but for our purposes we should start here, and not over complicate things.
Knowing which aberrations to correct
For example, depending on the optical configuration, not all aberrations need to be corrected. Some examples:
- Telescope objective: longitudinal chromatic aberration, transverse chromatic aberration, spherical aberration, coma
- Collimator lens: longitudinal chromatic aberration, spherical aberration, coma
- Eyepieces: longitudinal chromatic aberration, transverse chromatic aberration, astigmatism, field curvature, maybe distortion (depending on the field of view)
- Camera lenses: all seven (and most certainly more for modern lenses)
- Microscope objective: both chromatic aberrations, spherical aberration, coma.
It’s really important to know the optical system and its requirements, because you don’t want to correct for an aberration that doesn’t affect the system in any way.
Chromatic aberration and correction
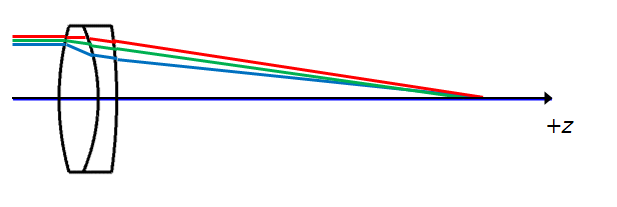
The first aberration we are going to look at it chromatic aberration. I choose this one first because as I mentioned above, it can be calculated in first order, as an extension of Gaussian or 1st order optics. Different wavelengths have different index of refraction in the material (or dispersion), so we have to take account for the focus change that occurs with different wavelengths. Shorter wavelengths have a higher index of refraction than longer wavelengths, and it is not linear.
In the image below, we see rays passing through a positive lens. The C line, or red, focuses at a position farther away from the lens than say, the d line, or yellow (and green, for that matter). Conversely, the g line, or blue, has its focus point closer to the lens than the d line.
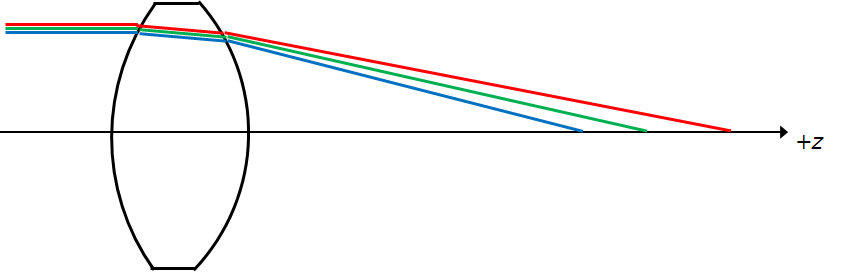
This is axial or longitudinal chromatic aberration, and different colours have different focal points.
To calculate this, all we have to do is use the spreadsheet raytrace and do that for different colour, i.e., different index of refraction.
We can plot the chromatic aberration with the following data.
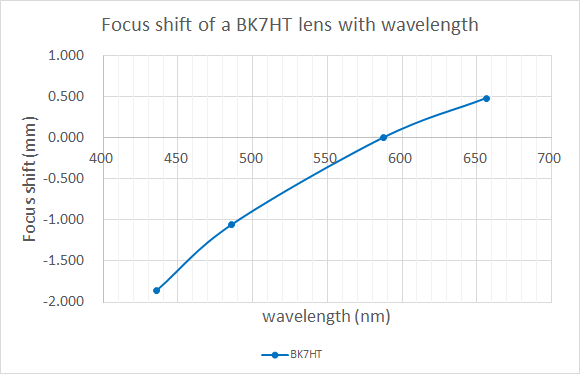
Transverse chromatic aberration is when rays refract to different heights or y direction positions.
Colour correction
Even if the image is perfect for one wavelength, there could be problems with the other wavelengths that make the image poor. This results in an image that is, for example, has fringes of different colours in the image. Even black and white photos are not immune, because the image will be blurred.
Historically, first there was isolating wavelengths, and then measuring the index of refraction for these spectra was possible. With this information is was discovered that colour can be corrected by using refraction.
The power \(\phi\) of a thin lens is represented as follows:
\[
\phi = (n-1) (1/R_1 + 1/R_2) = 1/f\\
C_1 = 1/R_1, C_2 = 1/R_2\\
TC = C_1 + C_2
\]
Where \(\phi\) is the lens power, f is the focal length. n is the index of refraction, \(C = 1/R\) is the lens curvature, t is the lens thickness.
Total curvature,\(TC = C_1 + C_2\) is mentioned here. Much like the diagram below, keeping TC the same while changing the lens shape is referred to as lens bending.
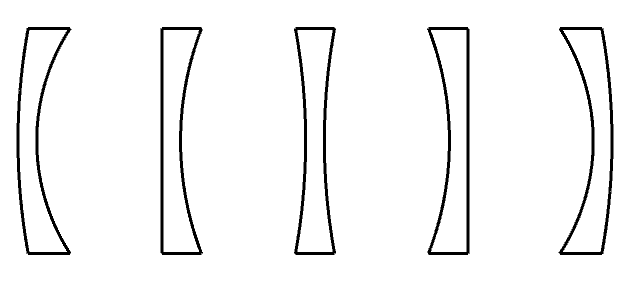
As we will see later with the triplet, this does not change the chromatic aberration. It also does not change the Petzval radius. But it does change the spherical aberration, for example. Bending can be used to balance the 3rd order aberrations while not chaining the chromatic aberration or the overall focal length of the lens. Although index of refraction plays a part in the power of the lens, the curvature of the lens plays a much larger role.
What the masters of the past used to do was solve the system for a fixed focal length of 1 or 100, and merely scale to lens to the focal length of their liking afterwards. Depending on the situation, 1 or 100 can make solving the equations much easier. This is called normalization, and if you’re familiar with old patents you may have seen this notation before.
To correct the colour, a common method is to use a positive lens with low dispersion or crown lens, with a negative lens with high dispersion or flint lens as a cemented doublet. Like in the diagram below, the F, d, and g lines line up much better than a simple positive lens.
(A little exaggerated for effect)
This is because the negative lens will spread the colours in the opposite direction than the positive lens, but will do so stronger due to higher dispersion, and the overall balance cancels each other out.
$$
\phi = \phi_1 + \phi_2 \\
L_{ch} = \phi_1/\nu_1 + \phi_2/\nu_2
$$
These two equations can be solved to figure out what the power balance of the crown and flint should be in order to cancel out the chromatic aberration, for a desired focal length.
One caveat is that this equation assumes a thin lens, so it works much better for relatively long focal lengths compared to the thickness of the lenses.
\(\nu\) is the Abbe number, calculated from the difference of index of refraction on wavelength.
$$
\nu = (n_d – 1)/(n_F – n_C)
$$
For example, a typical crown glass BK7 has an Abbe number of 64.1, while a typical flint glass SF2 has an Abbe number of 33.8. I’ve always wondered why the lower number has a higher dispersion, but Professor Abbe says so, so we’ll stick with it. Just like I had to accept that a charge of an electron is negative.
Here’s a spreadsheet calculation of a cemented doublet colour correction. The C1, C2, and TC are calculated. The target performance are f = 100mm, L_ch = 0. The starting points are R_1 = 60.03, and R_2 = -40.65. FK5 (nd = 1.4875, Abbe = 70.4) for glass 1, and F1 (nd = 1.6254, Abbe = 35.57) for glass 2 is used.
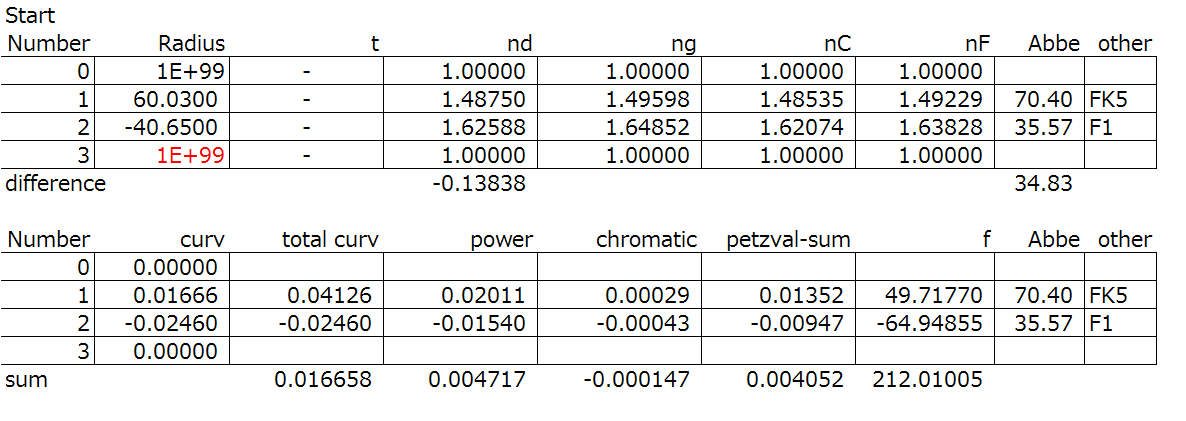
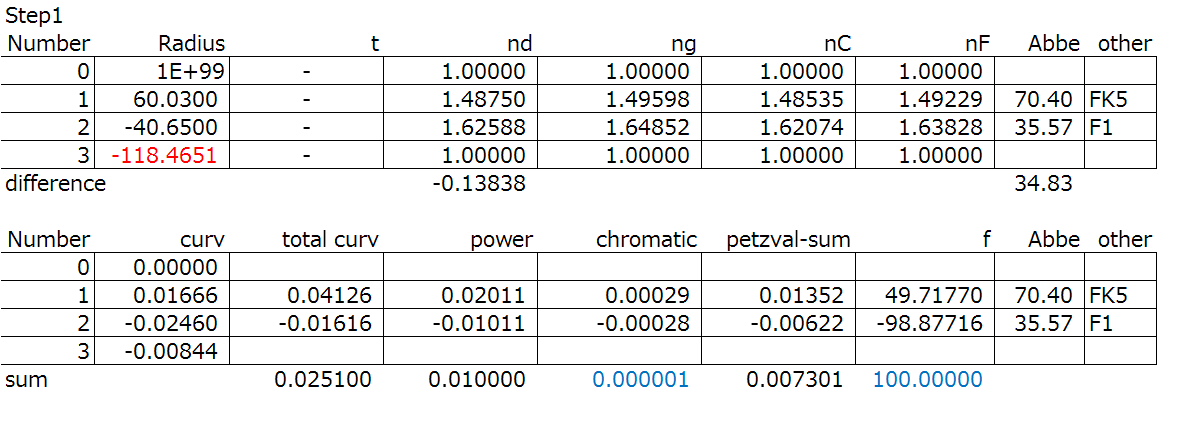
You can see in the “Step 1” that the radius of the last surface is calculated to minimize the longitudinal chromatic aberration.
Action Step:
Calculate C1, C2, and TC for a f = 100mm doublet lens, with a target chromatic aberration of Lch = -0.0015. Use starting points of R1 = 50, and R3 = -61.1. Use BK7 (nd = 1.51633, Abbe = 64.1) for glass 1, and SF10 (nd = 1.72825, Abbe = 28.5) for glass 2.
Achromat, apochromat, super apochromat
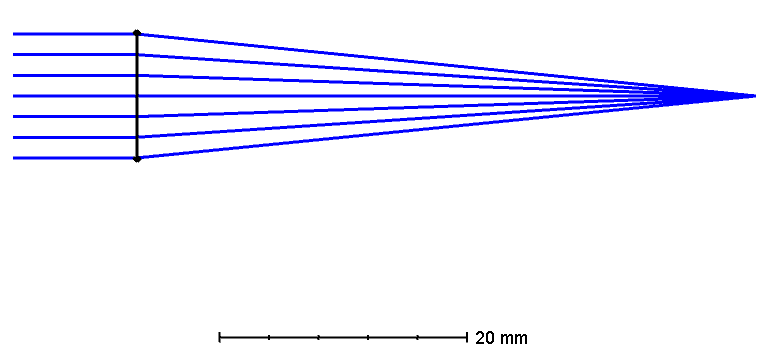
If you’re a photography nerd like me, you’ve heard of the terms APO, or achromat, or apochromat. We see them a lot in lenses.

(Leica Camera AG)
Shorthand, it is the following:
- Achromat: two wavelengths have the same back focal length in the optical system. Chroma is colour, and “A” means “not”, so the qualitative meaning is a lens with no aberrations from colour.
- Apochromat: three wavelengths have the same back focal length in the optical system. Some high end telephoto camera lenses and telescopes have this distinction.
- Super Apochromat: in addition to the three wavelengths, near infrared is also corrected.
Here are some graphical examples of the above colour corrected lenses, check out how many times each passes through the center “best focus”.
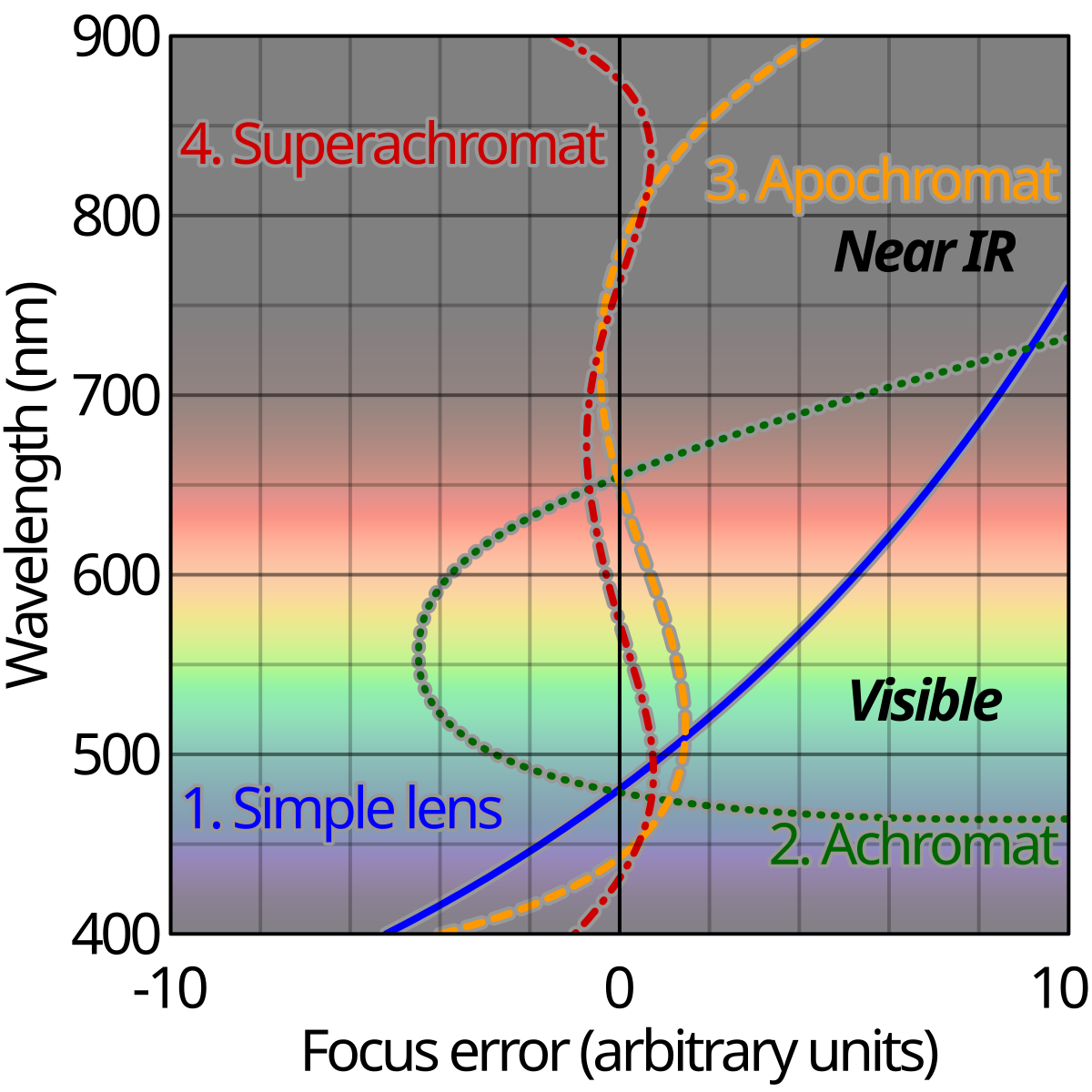
By Cmglee – Own work, CC BY-SA 3.0, Link
Spherical aberration
Spherical aberration is the first 3rd order aberration
Let’s revise the seven deadly aberrations:
- Axial or longitudinal chromatic aberration
- Lateral or transverse chromatic aberration
- Spherical aberration
- Coma
- Astigmatism
- Field curvature
- Distortion
Eventually we will have to get into other 3rd order aberrations, but spherical aberration is an essential place to start.
Here, I want to simplify these aberrations into spherical aberration, coma, and chromatic aberration so that an aplanatic lens design is possible. We want to look at simple lenses to look at the effects of these parameters a little more closely in a relatively isolated setting.
Why spherical aberration occurs
If we have a positive lens, and parallel beams pass though this lens, the light does not converge to one point. This is because as the rays pass a larger height of the lens, the ray angle increases, and the ray passes the optical axis closer to the lens.
This is the schematic description of spherical aberration.
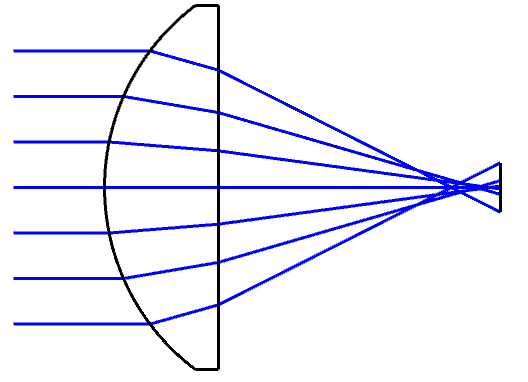
This means that with a positive lens, there is always spherical aberration. When the rays pass the optical axis closer to the lens, it is called under-corrected spherical aberration, and the opposite is over corrected spherical aberration. There is no way that a single spherical positive lens can correct spherical aberration to zero, or for that matter, achieve over corrected spherical aberration.
A simple but effective schematic and concise description on spherical aberration can be found in the Astrophysics section in Hyper Physics website for Georgia State University.
Methods to correct spherical aberration
Here are some examples to correct or minimize the spherical aberration.
- Use a double convex lens, where the radius ratio of the front surface to the rear surface is about 1:-6
- Higher index leads to larger radius R, which leads to smaller spherical aberration. For example, Si/Ge lenses for far infrared applications have small spherical aberrations
- Split the lenses, and the overall spherical aberration decreases. Splitting the lens in two splits the optical power of the system into two lenses, and we can use the radius ratio 1:-6 correction twice.
- Using flints. Cemented doublet, or a positive and negative lens suitably separated (like in the triplet lens)
- Kinda cheating, but an aspherical lens will decrease the spherical aberration. We won’t go into detail here.
- Aplanatic systems.
Spherical aberration is the most basic of aberrations, and requires attention as such. If demand and requests are high, I am considering going into spherical aberration in more detail at a later time.
Coffee break: Bokeh – out of focus blur
The term bokeh has become almost universally known in the English speaking photography community as a term for “out of focus blur”. There was a funny story about bokeh on The Online Photographer, stating that “in recent years Japanese photo writers have evidently decided they need a cool new loanword instead of bokeh, so one now often sees the fractured English expression outo fokasu.”
I’ve actually seen this a lot in online Japanese photography articles. “Outo” the Japanese phonetic pronunciation of “out”, and “fokasu”, the Japanese phonetic pronunciation of “focus”.
So English speakers are using a loanword from Japanese and the Japanese are using a loaner from English.
This is way too funny. I’ll end with a nice bow to the whole discussion.
By the way, the most sober term (in English) for what either means is “out-of-focus blur,” which of course has the disadvantage of being long, fussy, and annoying to type. I think “bokeh” and “outo fokasu” are more charming and whimsical.
Coma
Coma is the second 3rd order aberration
Coma aberration, or simply coma, is the second aberration that is usually studied after spherical aberration. Contrary to spherical aberration, which is a circularly concentric bokeh of the focus point, coma makes an off-axis point appearing to have a tail, or coma, like a comet.
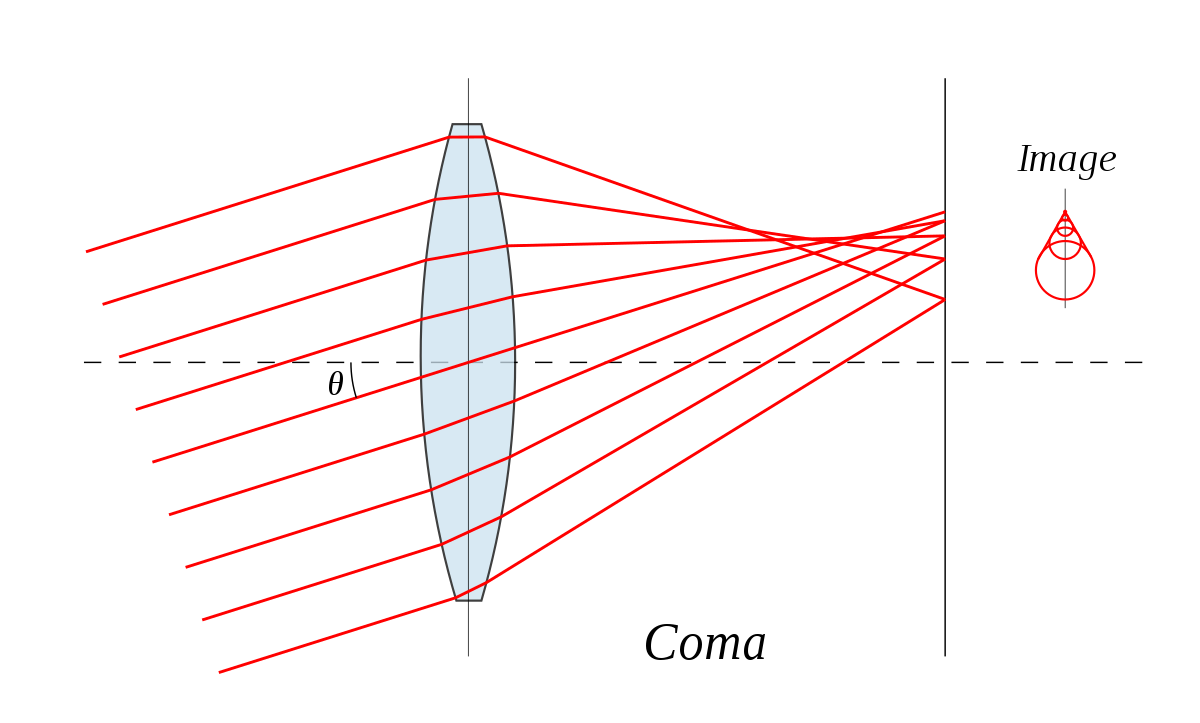
By http://upload.wikimedia.org/wikipedia/en/3/31/Lens-coma.svg, CC BY-SA 3.0, Link
As the rays pass a higher angle, the ring of the pupil traced to the image plane is larger than an intermediate ring near the center of the entrance pupil. The superposition of all the rings result in a comet like shape.
In the image below, the upper ray bends with a larger angle, and conversely, the lower ray bends with a smaller angle towards the image plane, and are not symmetric.
A simple but effective schematic and concise description on coma can be found in the Astrophysics section in Hyper Physics website for Georgia State University.
Coma-free conditions
Similarly to spherical aberration, there are various conditions that does not generate coma.
- Aplanatic systems: in essence a lens that does not have spherical aberration and coma is said to be aplanatic.
- Abbe Sine condition: a condition where the sine of the output angle is proportionate to the input angle.
- Concentric lens systems: An optical system where the rays enter perpendicular to the optical surface is. For example, the Ross concentric lens.
- Unit magnification optical system: A unit magnification system has a magnification of one. This idea was used to make many closely symmetric lenses such as the double gauss to reduce coma.
There are higher orders of coma, and the images can look very complicated. Even in modern lenses, most of the time the aberration that seem the most pronounced is usually the coma.
Thin lens 3rd order bending effects on spherical aberration and coma
We’ve looked at first order Gaussian optics before, simplifying the sine of an angle. The Taylor expression of the sine of an angle is as follows:
$$
\sin u = u – u^3/6 + u^5/120 …
$$
Taking the first term, or \(\sin u = u\), first order or Gaussian optics, and has no aberration. Taking the second term, \(\sin u = u – u^3/6\), is the basis of 3rd order aberration theory. Taking the third term, up to \(u^5\), is 5th order aberration theory. Take the entire sine function, and you’ve considered the aberration completely.
Even in 3rd order aberration theory, taking the lens thicknesses to zero is thin lens 3rd order aberration theory in lens design. And the simplest regression of this format is making the stop on the lens surface.
This is where the spherical aberration can be expressed as a quadratic function and the coma as a linear function, with respect to the bending of the lens.
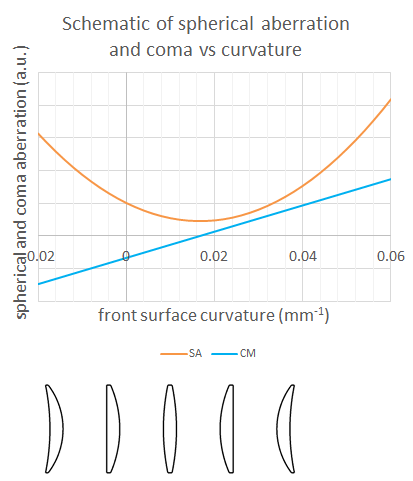
Although the spherical aberration is not zero, it is at a minimum, and the coma is at zero. This is a useful qualitative property to remember.
Telescope objective lens design
Why telescope objectives are important and useful
We’ve explored raytracing. We’ve explored colour correction. We’ve looked at two monochromatic aberrations.
What we need to correct in a telescope objective is
The general system of a telescope objective is used in many applications. Obviously the telescope, but also laser beam collimators, CD/DVD/Blu-ray lenses, and relay lenses.
However, the objective (pun intended) for optimizing the telescope objective lens design is not to correct the above three aberrations, but it is to balance them to certain criteria. This is an important concept throughout optical lens design with aberrations, the goal is most often not to completely correct all the aberrations in the system, but to keep certain aberrations at designated values. This technique can be seen in many lens designs, most notably the zoom lens design, where each group is kept at a certain aberration to balance with the rest of the system.
If we use cemented lenses intelligently, we can control the higher order aberrations. This is a common practice in many lens designs. At the same time, using cemented lenses is not trivial to express, and also not quantifiable in an equation or a theorem. This choosing of cemented lenses is the very reason why lens design itself is as difficult as it is, but a good lens design cannot be achieved without proper knowledge of this subject. The irony.
The astronomical and mathematical giants like Jean le Rond d’Alambert, William Herschel, Peter Barlow, Joseph Johann von Littrow, Leonhard Euler, Carl Friedrich Gauss, Carl August von Steinheil, Joseph von Fraunhofer all studied lens design and how to effectively use cemented doublets.
Therefore, my feeling is that going through the classical method of telescope objective design is a perfect way to see the history of lens design unfold in front of us. The system is simple enough to concentrate on the aberrations, while being complicate enough to learn deeply.
Coffee break: The dawn of the telescope
There is an interesting story about the telescope in Optics by Eugene Hecht, where the first telescope could have been studied as early as the 14th century, since spectacles were invented then. But the earliest documented telescope invention is October 2nd, 1608, where Hans Lippershey was rejected of his patent for a telescope.
Think about it, the telescope, in 1608? What kind of military advantages could be had for country that has a device possible of seeing long distances, compared to a country that doesn’t? The patent was rejected and the government purchased the rights to the invention.
The story doesn’t end there, Galileo Galilei heard of Lippershey’s work, and by 1609 Galileo made a telescope with two lenses and an organ pipe for a tube. This is a Galilean telescope, by the way.
I think it’s interesting that Galileo’s famous studies on Astronomy was based on a invention that he only sparse information on, and improved it to the point where people sought after it. Although Galileo’s methods may be extremely primitive compared to what we have today, I think we can consider him to be a lens design, just like us. As an aside, the teleskopos is a Greek term for seeing a distance.
Cemented telescope objective lens design

The lens is extremely close to a thin lens, so the thickness of the lens does not affect the performance in a significant way. The larger effects are the three radius of curvature, which give us three degrees of freedom to correct the focal length, the spherical aberration, chromatic aberration.
In a nutshell:
- Choose glass
- Solve the thin lens colour correction
- Choose the radius R by suitable curvature of the lens
- Choose a suitable thickness of the lens based on the thickness of the edge, and ease of polishing. Raytrace, fix the focal lens to be the same as in the previous step
- The target chromatic aberration is achieved by changing R2, and using R3 to adjust the focal length. By finding how the chromatic aberration changes with the change in R2, we can get our desired chromatic aberration
- Use bending technique to get the desired spherical aberration
Step 1: Choose a suitable glass combination for an achromatic doublet, evaluate chromatic.
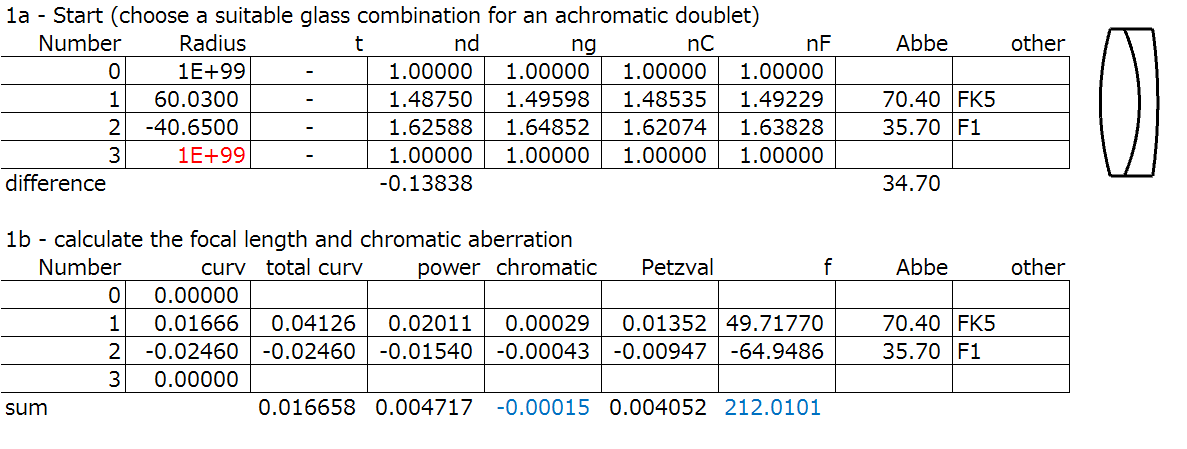
Step 2: Solve the thin lens colour correction, as we did in the colour correction section.
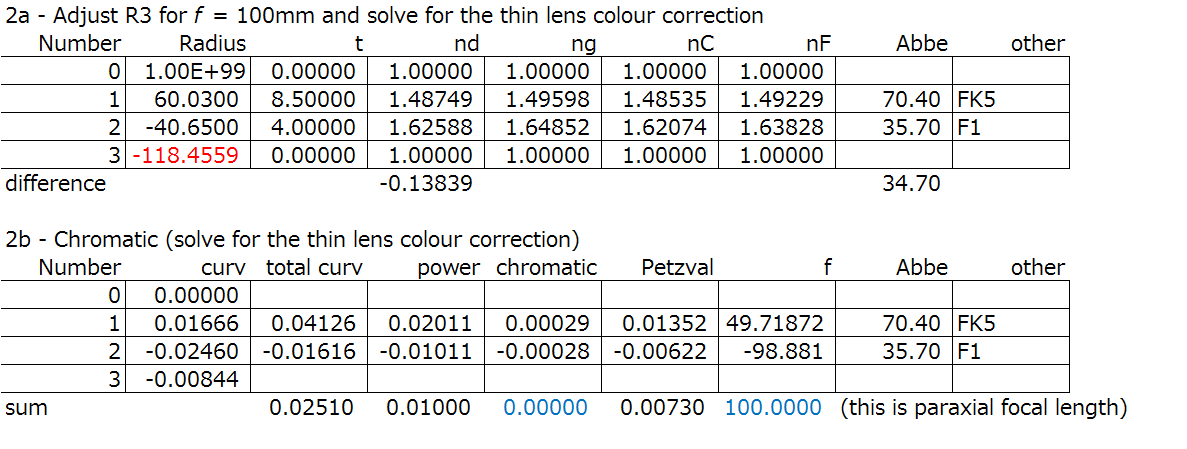
Step 3: Perform the paraxial raytrace, or YNU raytrace.
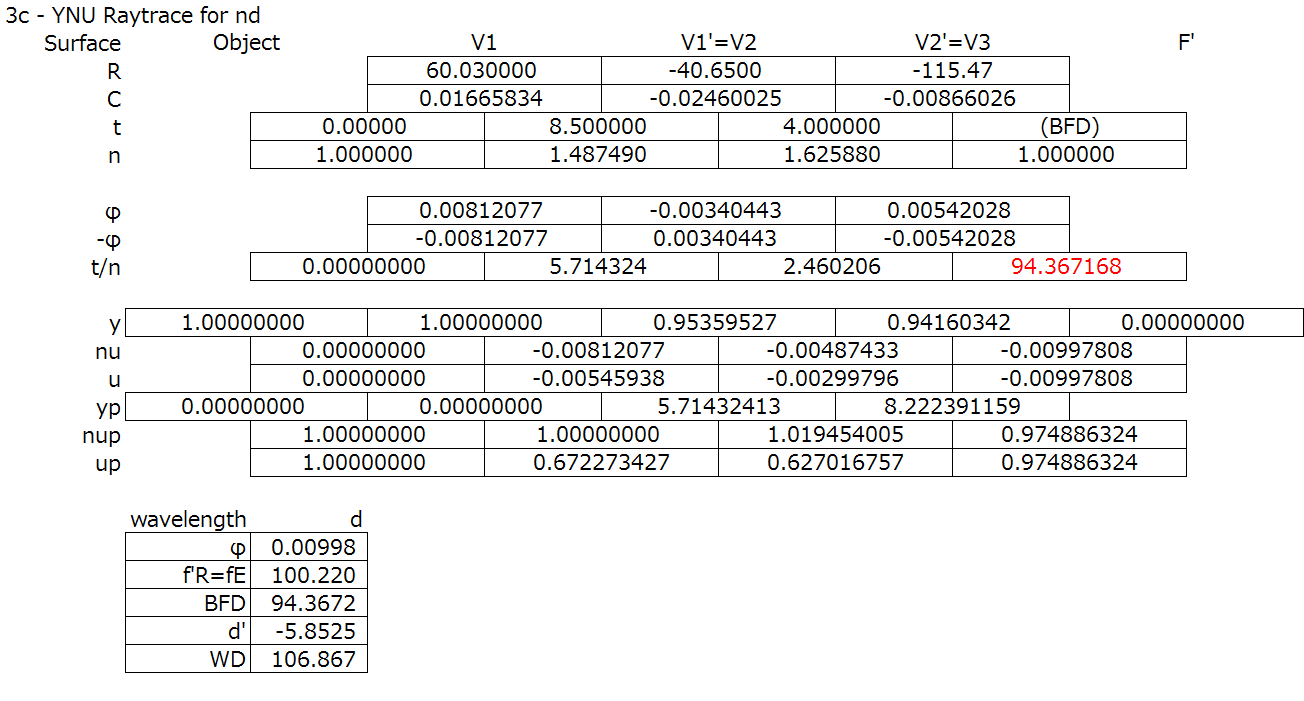
(Here’s the corresponding lens shape and chromatic, BTW)
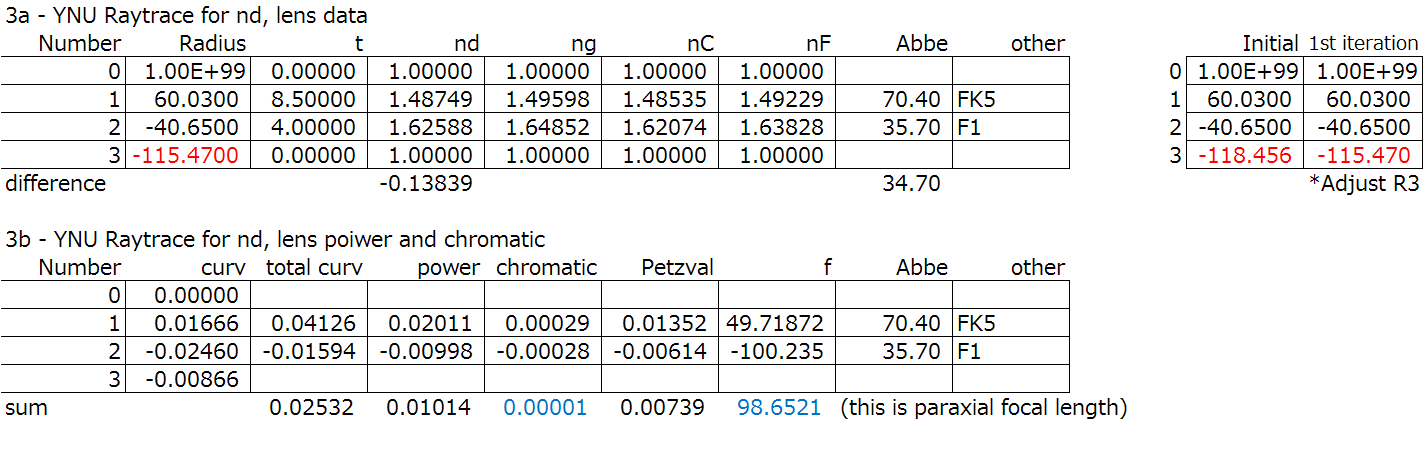
Step 4: To make things simple, we can normalize the focal length. This comes in handy when we compare lens systems. We can also perform the normalized colour correction.
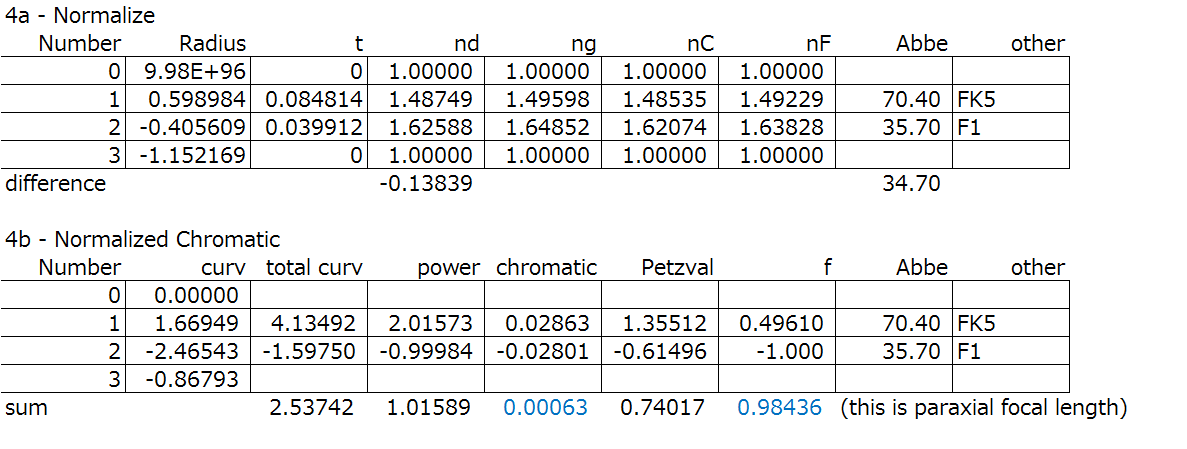
Step 5: Perform the paraxial raytrace, or YNU raytrace for the normalized system.

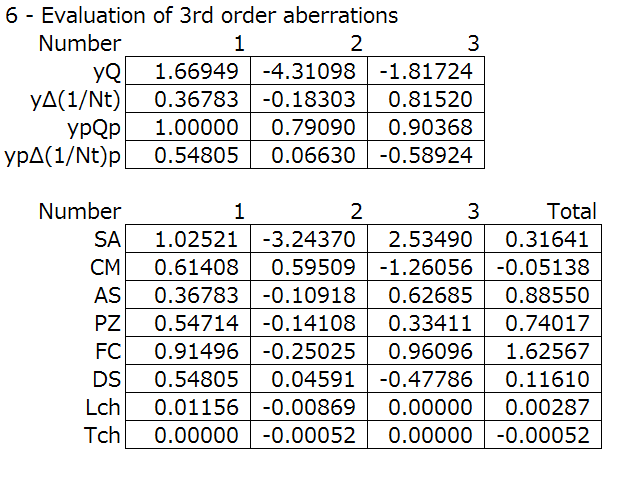
Step 6: Evaluate the 3rd order aberrations.
So what about coma, second order chromatic aberration, and higher orders of spherical aberration? They’re all important for telescopes, right? Well, those aberrations were automatically chosen once we chose the index of refraction and the Abbe number for the two lenses.
The giants of lens design did extensive research on this topic, but there is still no definitive answer, which makes lens design all that more difficult, and to me, all that more attractive. Testing multiple glass types with each other and comparing our answers with the research of the giants can help us immensely with our craft.
3rd order aberrations – spherical aberration, coma, astigmatism, distortion, Petzval sum
Although there are several calculations that we need to do for the aberration calculations, I’ve listed them here, sans derivations. Each one is simple to calculate in a spreadsheet.
The initial conditions are set up as follows:
If the focal length is normalized to 1, things are easy to compare.
y1 = 1, nu1 = 0 is the start of the paraxial marginal raytrace.
yp1 = –EP, nup1 = 1 is the start of the paraxial chief ray trace.
Where EP is the entrance pupil position, calculated by reverse raytracing.
The preliminary equations are as follows:
$$
y Q = (y n)/R – nu \\
y_p Q_p = (y_p n)/R – nu_p \\
y \Delta (1/nt) = u’/n’ – u/n \\
J = (y_p Q_p)/(y Q) \\
PZ = \phi/(n’n)
$$
Where y is the marginal ray height, ypis the chief ray height, n is the index of refraction, u is the angle, and PZ is the Petzval sum component for each surface. The prime in u’, for example, is the angle of the refracted ray relative to the surface.
The 3rd order aberrations can be calculated as:
$$
SA = y [(y Q)^2] \times [y \Delta (1/nt)] \\
CM = J \times SA \\
AS = J \times CM \\
FC = AS + PZ \\
DS = J \times FC
$$
Where SA= spherical aberration, CM= coma, AS= astigmatism, FC= field curvature, DS= Distortion.
(We can gloss over astigmatism, Petzval sum, field curvature, distortion, and transverse chromatic aberration for now, because they can’t be corrected for a doublet telescope objective. We will get into more detail later, when they become more important)
These aberrations are calculated for each surface, and then are added together for the entire system. The key here is each surface, not the end sum, so we can observe the aberrations on each lens.
Let’s take a look at the Step 6 results again, the evaluation of the 3rd order aberrations.

Action Step:
Use a spreadsheet and design a cemented telescope objective, calculate the 3rd order aberrations.
Even better, download the spreadsheets used in this Guide!

Get Your FREE Lens Design Guide with Spreadsheets
Enter your name and email for instant access to our Guide to Classic Lens Design (in PDF format) and the actual spreadsheets used in the guide!
??100% privacy, and we hate spam. When you sign up, we'll keep you updated usually with one email per week, occasionally up to a few times a week. Unsubscribe at any time.
Let’s look at the results in detail.
We have the spherical aberration under corrected at the 1st surface and the 3rd surface, which is slightly larger. The cemented surface, i.e., the 2nd surface overcorrects the spherical aberration, and cancels it out overall.
The coma is different as it is positive for the 1st and 2nd surfaces while it is negative for the 3rd surface.
Now I haven’t mentioned much about astigmatism, field curvature, and distortion. For distortion, in a small field like this system, you can see from the results that it is small.
Astigmatism and distortion, you can see is governed by the power of the lens, and can’t be changed by bending. Also, since the field curvature is dependant on the Petzval sum, we see that it is governed by the choice of glass and the power of the lens, and not the curvature.
Knowing these properties will help when designing. For this case, it’d be a futile attempt to try to correct the astigmatism and the field curvature by changing the curvature of the lens at this stage. This knowledge comes in handy for more complex systems if we break them down.
Also, you can see that the field has a very small effect in the paraxial— and the coma, astigmatism, field curvature, and distortion have larger effects, in that order, as the field gets larger. Conversely, in the paraxial, the largest aberration is spherical aberration, and is smaller in the same order, the coma, astigmatism, field curvature, and distortion.
By looking at the equations, we can see that coma is essentially something added on to the spherical aberration, and so when the spherical aberration is small, most of the other aberrations become smaller as a result. This means that the spherical aberration is usually the first one to correct. This is common in many optical systems.
The difference between understanding and not understanding the third order aberrations makes a huge difference when doing lens design. It’s essentially the difference between designing a lens with a map and knowing where you’re going, and designing a lens blindly.
Separated telescope objective lens design
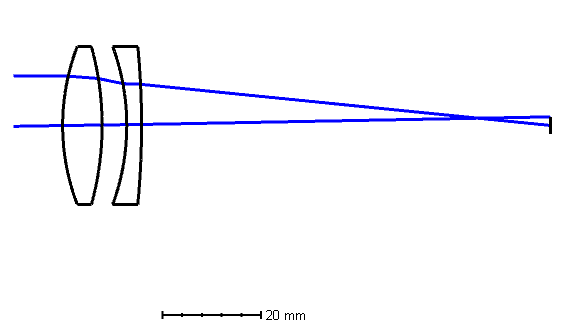
Now, we already looked at the cemented doublet, but simply separating the lens into two lenses, we get two degrees of freedom. Namely, the lens bending of the entire system, and the lens bending of the negative lens alone. This added degree of freedom allows us to control the coma more freely than before.
However, as soon as there are two lenses that are not cemented, we have to think about the lateral displacement of the lenses, and the separation of the lenses, so the tolerance is much more difficult to overcome. So there are some consequences.
A rough flow of the lens design is done as follows:
- Choosing glass
- Not the easiest process, take the massive library of the giants before us for suitable choices. Also try the Harting method for choosing glass
- Thin lens focal length adjustment, colour correction
- Can calculate solutions easily with equations
- Provides guidance for the actual lens design
- First order lens design, thick lens colour correction
- Requires raytracing
- Evaluate the 3rd order aberrations and make corrections
- Can evaluate quickly
- It is completely independent from the 5th order aberrations and the chromatic aberrations
- We can see the contributions from each surface clearly
- We can strategize which aberrations to correct
- We can try to minimize the contributions from each surface, and not just the total aberration
- This is advantageous for a loosely toleranced design
- We can suppress the effects higher order aberrations and balance the system
- (If you have Zemax/Code V) Raytrace the system and optimize
- High precision raytracing and evaluation
- Can lead to great results if you know the inner workings of the optical system
- Trial and error process
- Need a computer, potentially expensive software
- (If you have Zemax/Code V) Evaluation of the optical performance
- Wavefront aberration evaluation
- Optical Transfer Function (OTF) evaluation
- Spot diagram, etc.
- Tolerancing
- Need a computer, potentially expensive software
Let’s look at how lens design fares with a spreadsheet for a separated two lens telescope objective. Logically speaking, we can get to the 3rd order aberration correction step.
However, even when utilizing ray tracing, we already know from 3rd order aberration analysis which way the aberrations change and affect each other, so the path to a better design is already laid out. Think of the 3rd order aberrations as a compass to guide us along the right path.
For the thin lens calculations, the following are useful assumptions and calculations:
- Thickness \(t = 0\)
- focal length \(\phi = 1/f = (n-1)tc\)
- \(tc = c_1 – c_2 = 1/R_1 – 1/R_2\)
- colour correction \(chr = \phi_1/\nu_1 + \phi_2/\nu_2\)
- Petzval sum \(P = \phi_1/n_1 + \phi_2/n_2\)
- bending (change \(c_1\) and \(c_2\) without changing \(tc\))
It is important to track our results as we go, and repetitions of this method will refine our understanding of lens design.
In a nutshell:
- Choose glass
- Solve the thin lens colour correction
- Choose the radius R by suitable curvature of the lens
- Choose a suitable thickness of the lens, raytrace for colour analysis
The target chromatic aberration is achieved by changing R2, and using R3 to adjust the focal length. By finding how the chromatic aberration changes with the change in R2, we can get our desired chromatic aberration. We will also use the lens bending technique to get the desired spherical aberration.
Step 1: Choose a suitable glass combination for an achromatic doublet, evaluate chromatic.
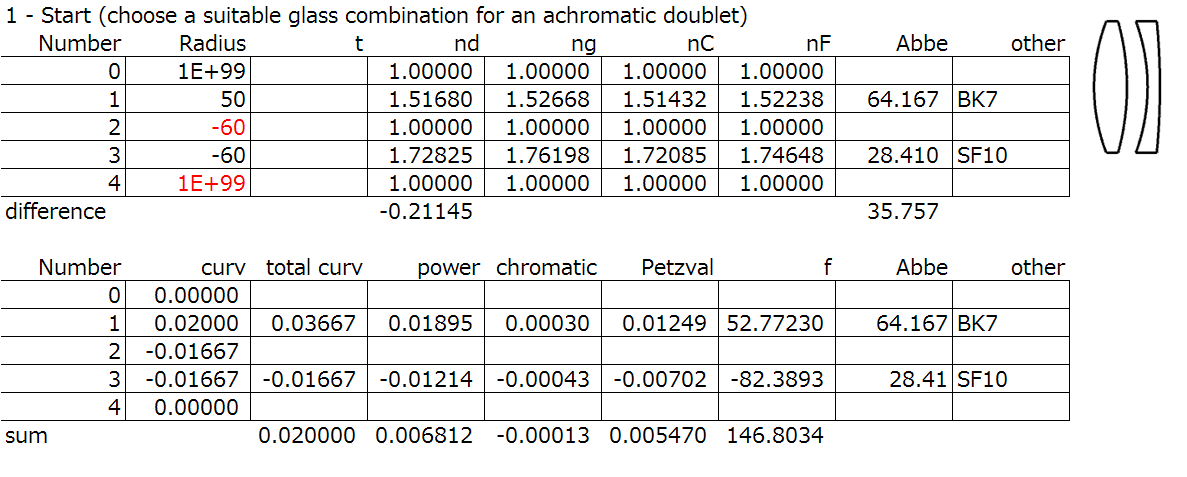
This step isn’t as easy as it seems, and there have been great studies by Dr. H. Harting (Zeitschrift fiir Instrumentenkunde, vol. xix. p. 269 (1899) and vol. xviii. p. 357(1898)), the designer of the famous Heliar lens for Voigtländer (now produced by Cosina. Even as recent as 1996, achromatic doublet glass choice has been studied.
Step 2: Solve the thin lens colour correction, as we did in the colour correction section.
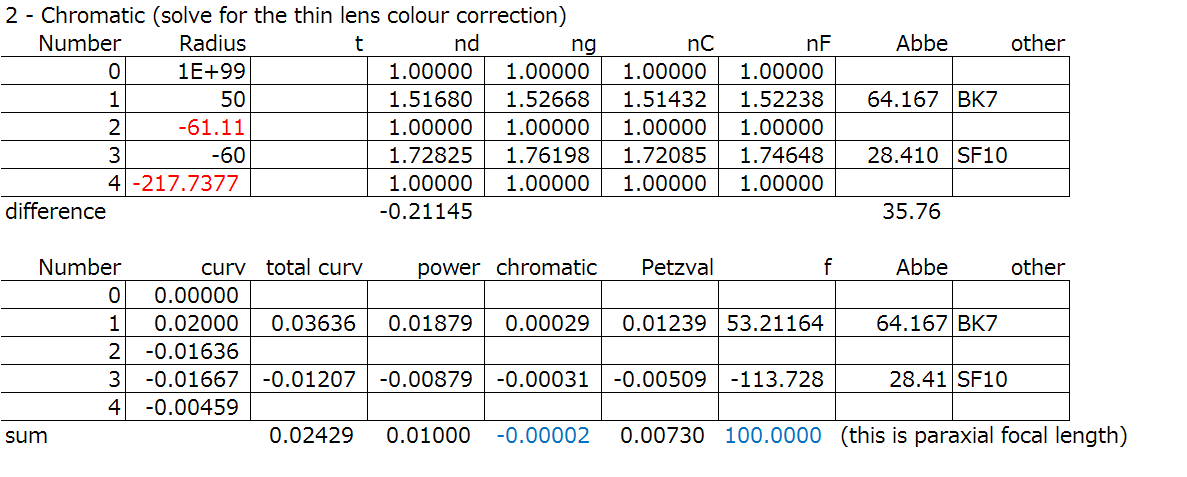
Step 3: Perform the paraxial raytrace, or YNU raytrace, evaluate and correct the colour.
First, the calculations from the results we got from step 2:
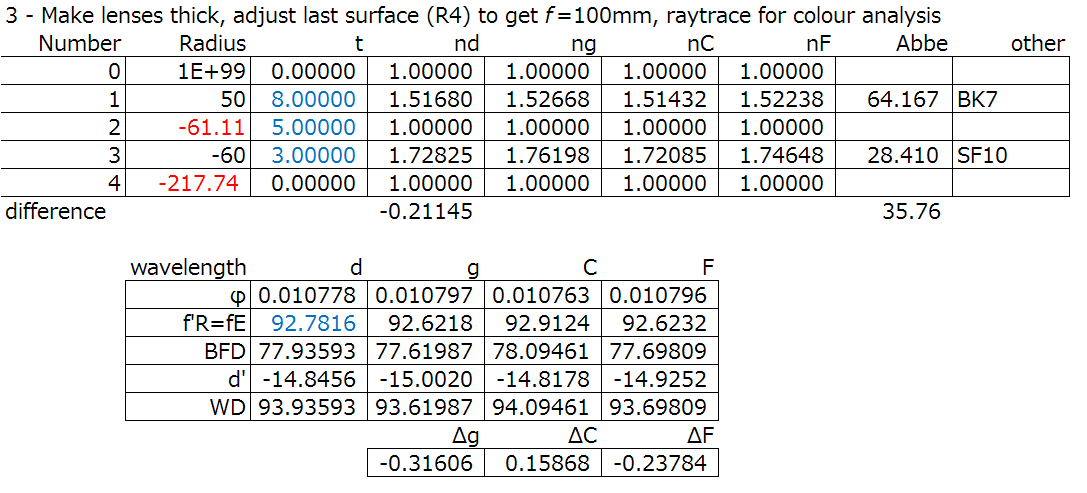
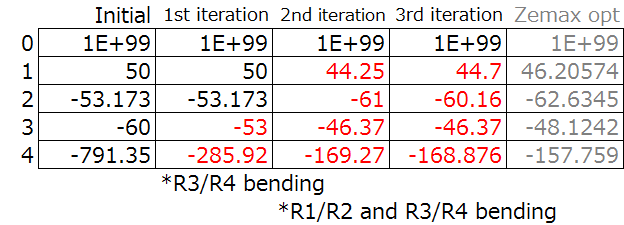
Here are the iterations I did for the shape, as I changed R2 and adjusted R4 to get the desired focal length and colour correction. In this case, it is optimizing the focal length difference between the d line and the other lines, g, C, and F.
And the results for the colour correction are as follows:
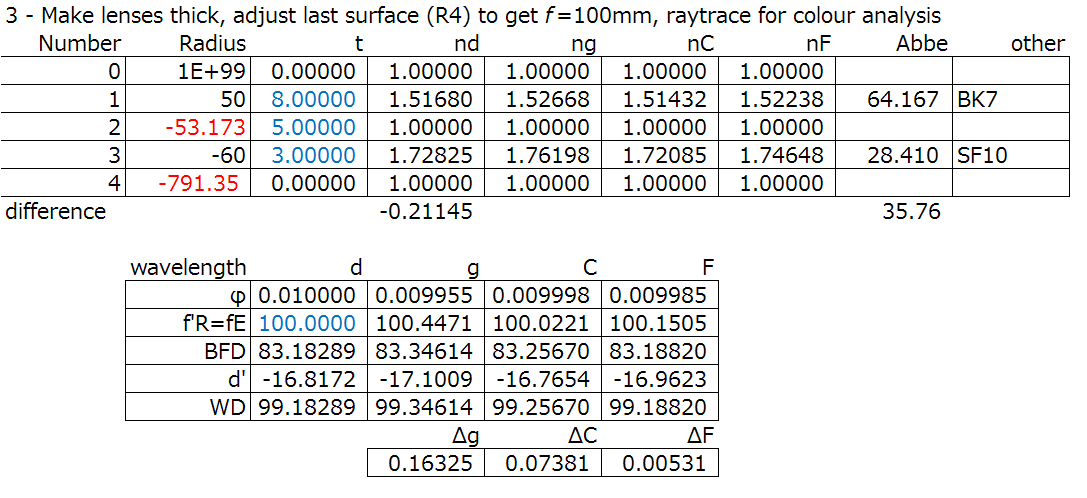
Step 4: Evaluate the 3rd order aberration correction, with normalization.
From the calculations we got in step 3, we can raytrace the system to calculate the aberrations.
First, setting up the 1st order system and normalization:
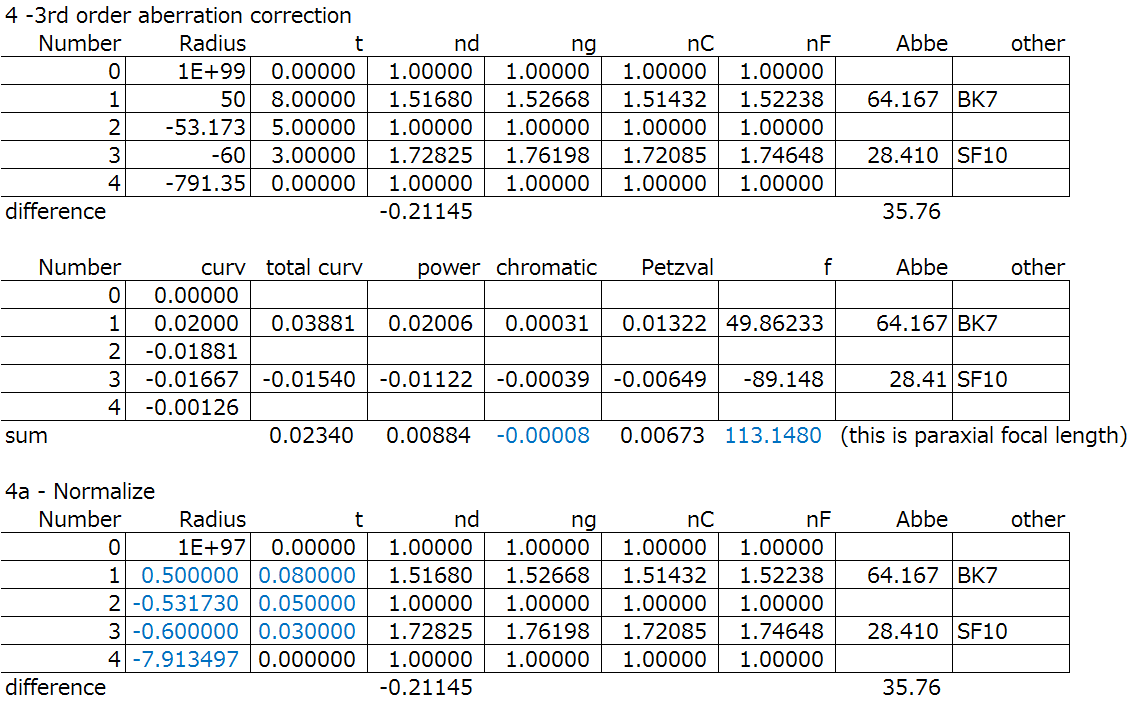
Next, the YNU raytrace:
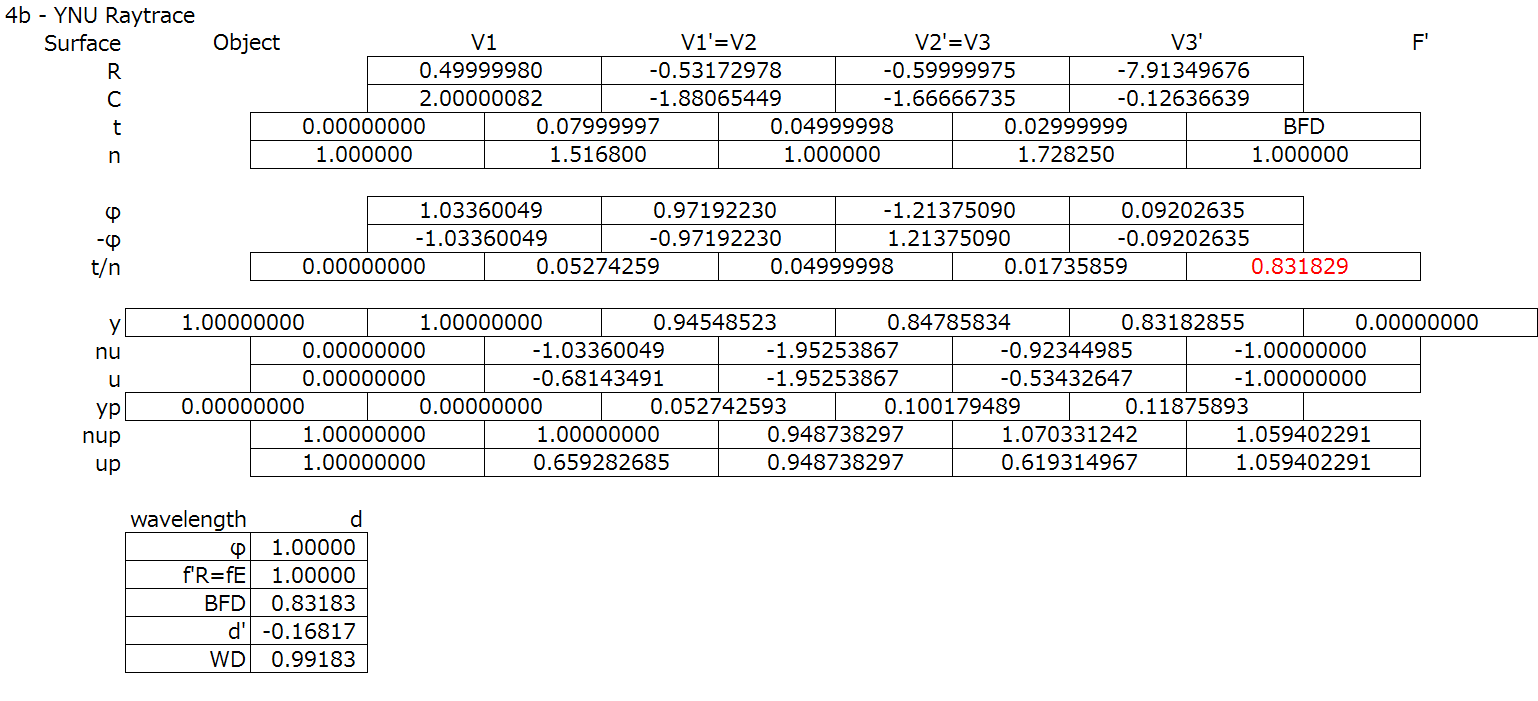
Finally, the evaluation of the 3rd order aberrations:
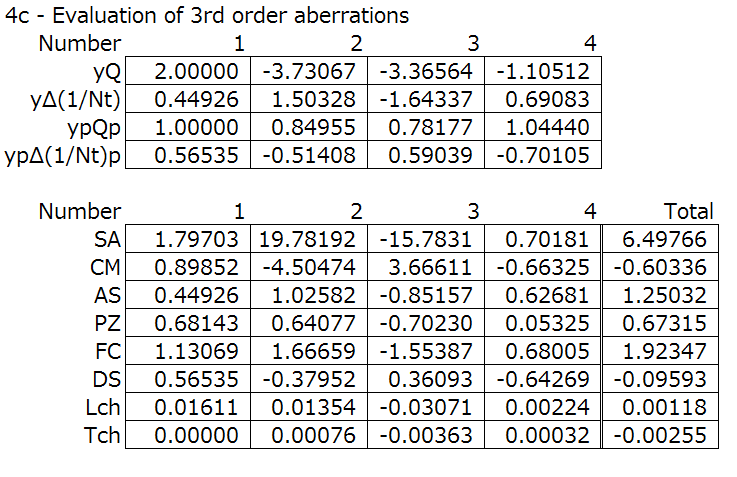
SA = spherical aberration, CM = coma, Lch = longitudinal chromatic aberration.
(We can gloss over the others for now, but for reference, AS = astigmatism, PZ = Petzval sum, FC = field curvature, DS = distortion, Tch = transverse chromatic aberration. These will come up later)
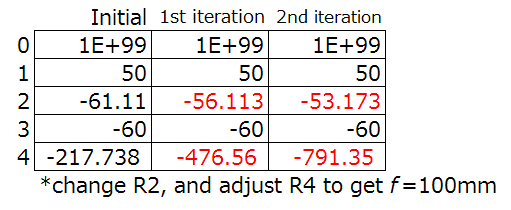
Step 4: Iteration one.
As a prerequisite, lens bending does not change the focal length of the chromatic aberration. Lens bending is changing the curvature of the surfaces of the lens while not changing the power (and therefore focal length) of the lens.
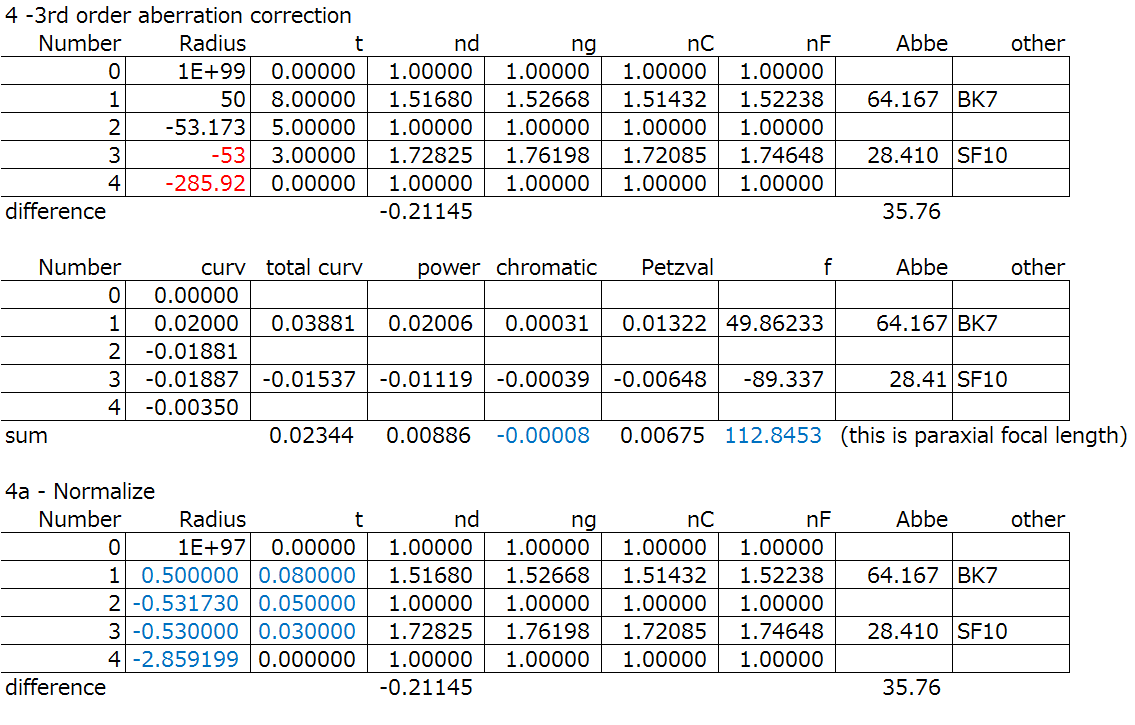
By lens bending the negative lens alone, we can overcorrect the spherical aberration in the negative lens (surfaces 3 and 4) to balance the entire system while not impacting the other aberrations. Look, the spherical aberration SA is better already.
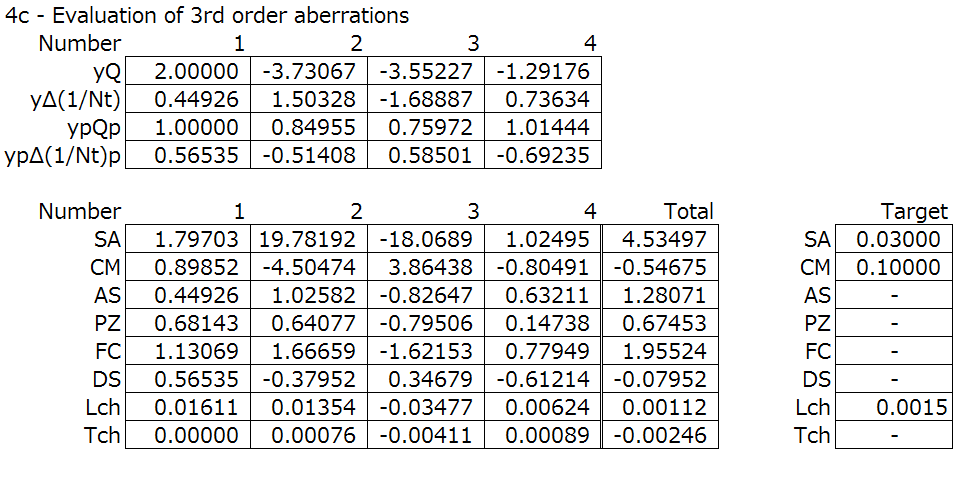
Step 4(continued): Iterations two and three.
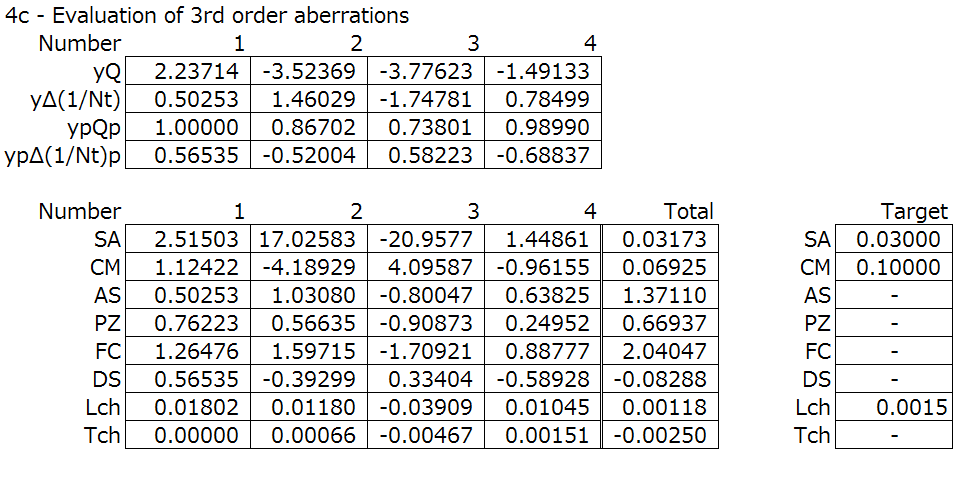
Increasing the curvature of the front lens will overcorrect the overall spherical aberration.
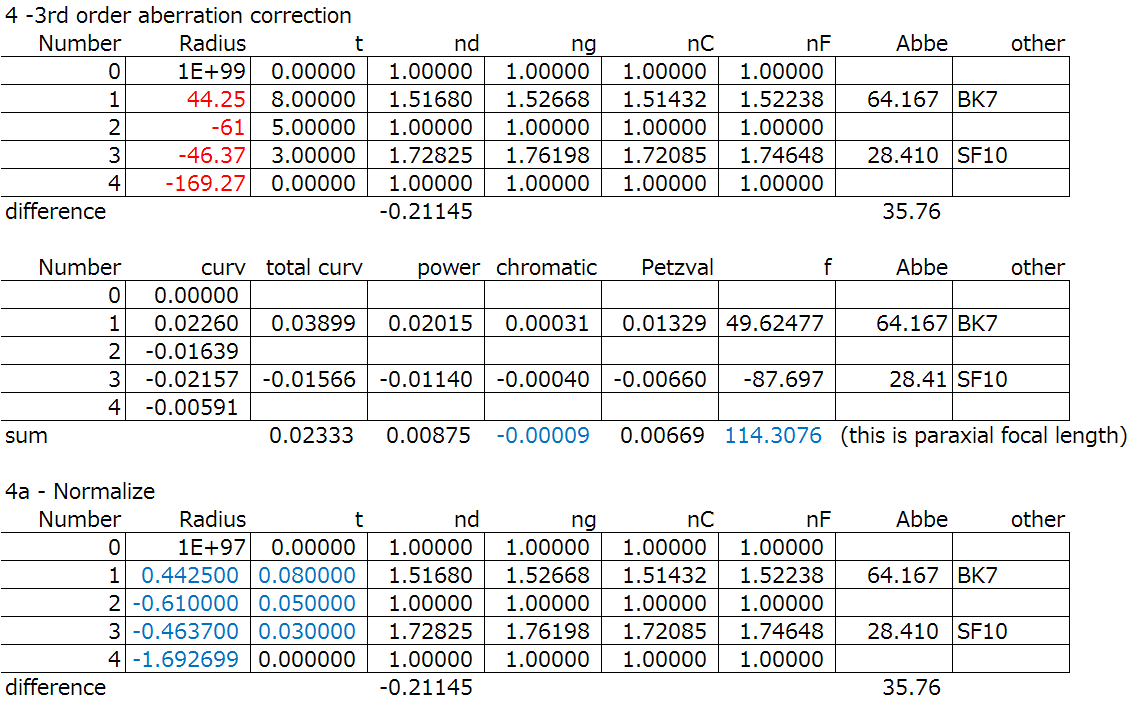
By lens bending the entire system, the coma can be controlled, and by increasing the front curvature the coma is under corrected. This obviously changes the spherical aberration, but the spherical aberration can be corrected by lens bending the negative lens to cancel it out. If we do both bending iteratively, the coma and spherical aberration will converge to the minimum.
Action Step:
Download the spreadsheet and design a separated telescope objective.
Even better, download the spreadsheets used in this Guide!

Get Your FREE Lens Design Guide with Spreadsheets
Enter your name and email for instant access to our Guide to Classic Lens Design (in PDF format) and the actual spreadsheets used in the guide!
??100% privacy, and we hate spam. When you sign up, we'll keep you updated usually with one email per week, occasionally up to a few times a week. Unsubscribe at any time.
Compare with Zemax
If you noticed the table with the iterations for the final lens shape, you’ll see the very right column has data from a Zemax optimization. I set up a simple system in the software and ran an optimization. The process was very easy for me since I’ve been using the software for over 10 years now, but if you’re starting Zemax from scratch, it won’t be as easy.
Some parameters, assumptions, and conditions for the Zemax lens design:
- Reasonable F/# of 5.0 (maybe 4.0 would have been more appropriate, but whatever)
- Half field of view of 1 degree, typical for a telescope objective
- Focal length 100mm
- Same glass as the spreadsheet (which means that Zemax didn’t choose the lens material for me)
- Same thickness of the lenses as the spreadsheet
- Made the radius of curvature R1 ~ R4 variable
- Set the merit function so that the a small spot size is a good result
- Ran the optimization about 5 to 10 cycles (I don’t remember the exact number)
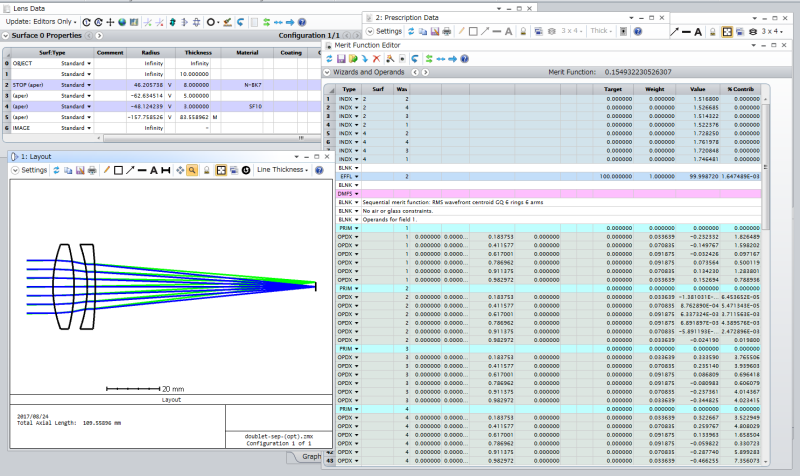
I plugged in the numbers for the radius of curvature that Zemax calculated, and looked at the spreadsheet.
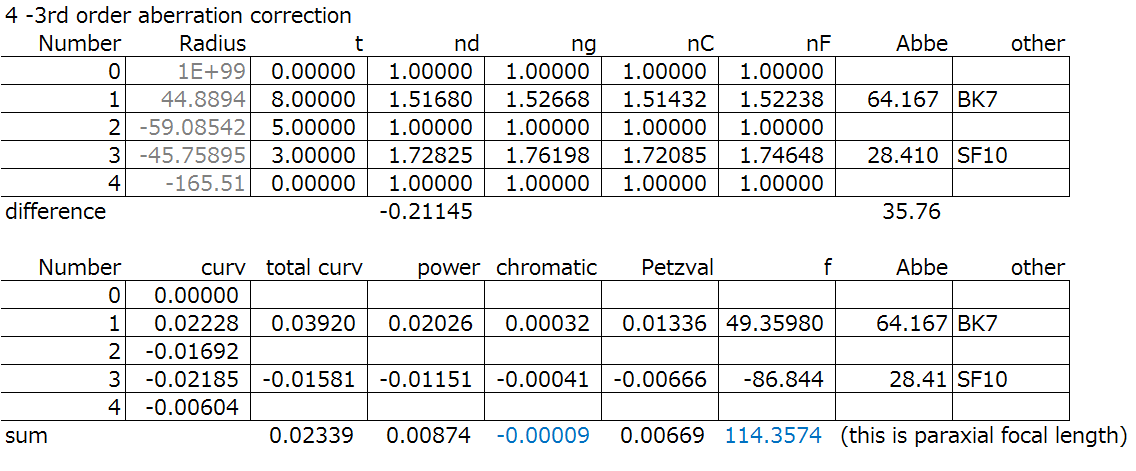
Hmmm… first order correction like colour seems to be the same.
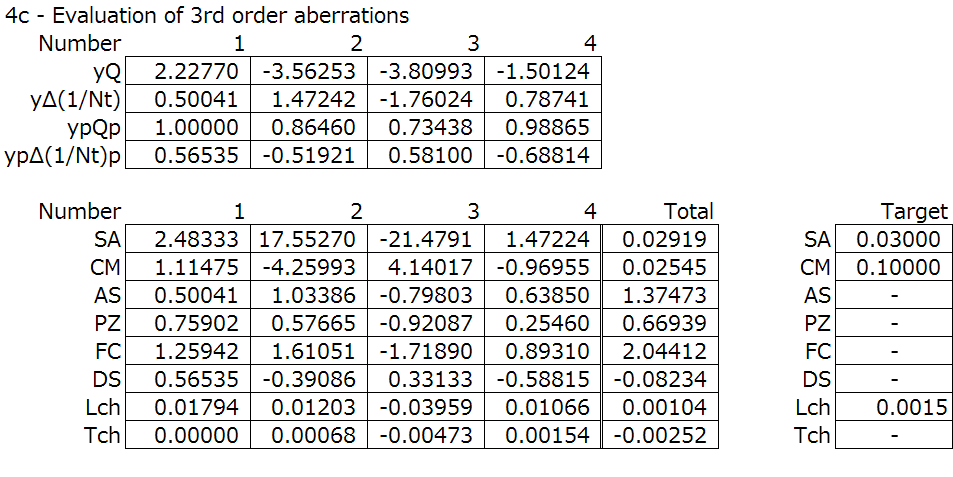
3rd order aberrations are similar too…
This leads me to think that when evaluating for 3rd order aberrations, the spreadsheet method and the Zemax optimization method are identical. I can’t correct the field curvature or the astigmatism even if I have Zemax, because of the properties of the lens system, which in this case is a doublet.
On the flip side, let’s take a look at how our separated telescope objective compared to the Zemax design in…. Zemax.
Separated telescope objective, designed by the spreadsheet method, evaluated in Zemax
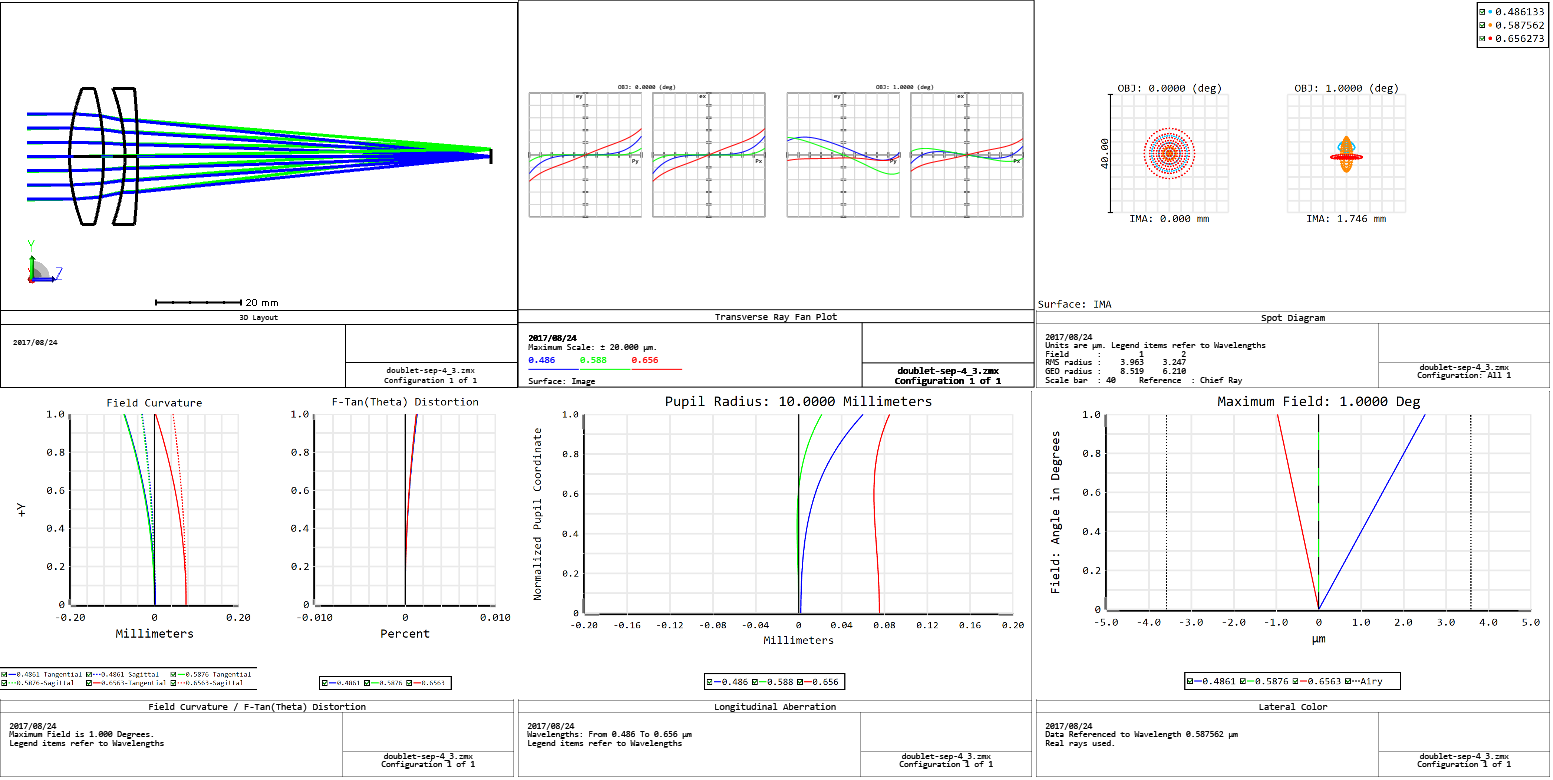
(Click to enlarge)
Separated telescope objective, designed in Zemax, evaluated in Zemax
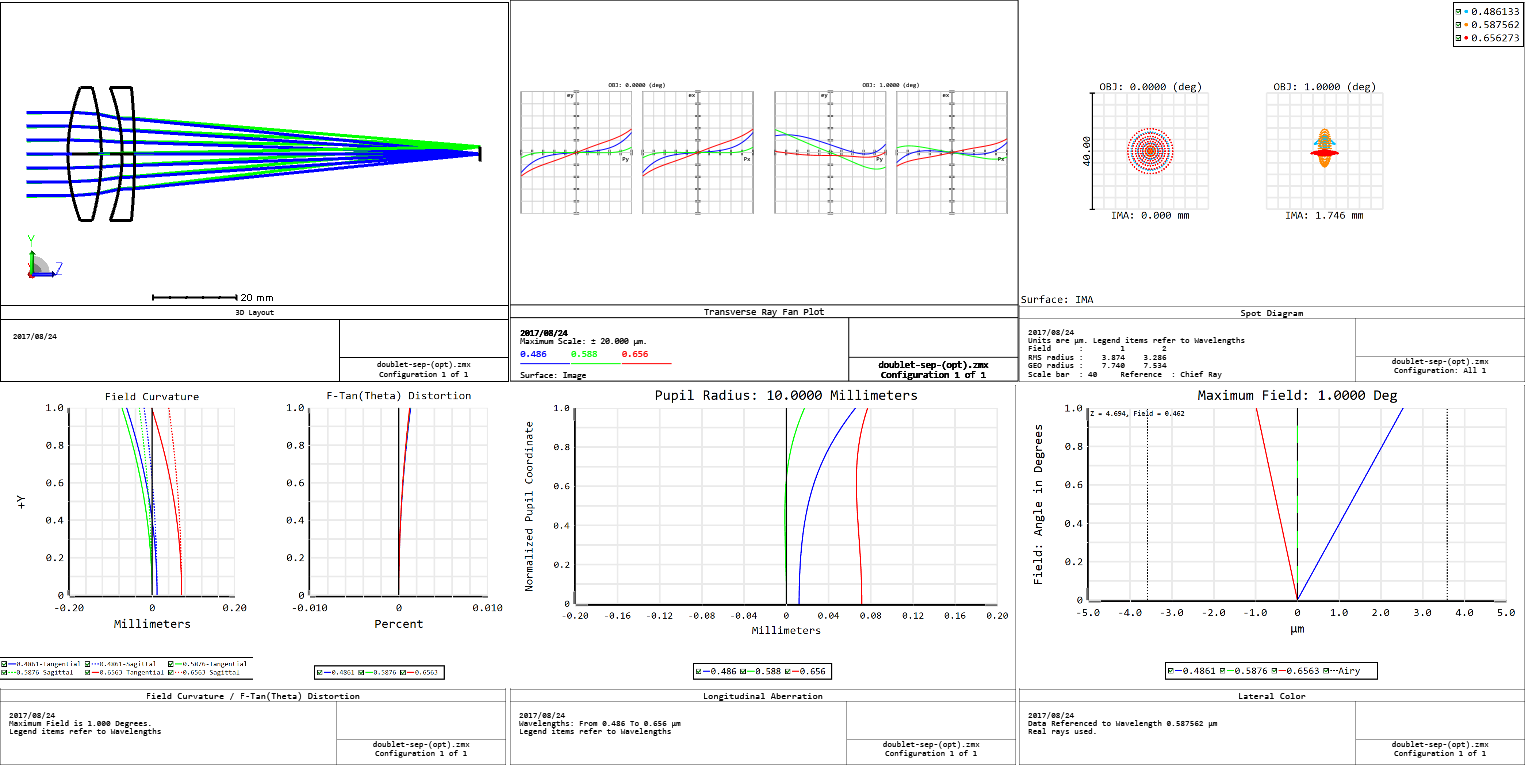
(Click to enlarge)
What I see:
- Ray fans are identical
- Spot sizes are identical
- Field curvature is identical, but the spreadsheet method places the marginal focus at zero
- Distortion is identical
- Longitudinal chromatic aberration is identical
- Transverse chromatic aberration is identical
What do you think? I think that the spreadsheet method with 3rd order aberration correction does remarkably well. But I think we learned a lot more by doing the calculations by hand. Now I’m not saying that we have to ditch our software and do our 24 lens zoom system by hand, but I do think that a lot of the concepts are lost when we use the software mindlessly.
Anastigmat lens design
We got deep into the process of lens design with the telescope objective, while looking at the key aberrations. This already gives us a leg up on what to look for in the lens system overall, and the effects of each surface going forward.
For a camera lens, the primary difference with the telescope objective is the field of view. The main effects of the higher field of view is the astigmatism and the field curvature.
Astigmatism and Petzval correction
With the aplanatic lens in the previous chapter, the uses are for telescope objectives or a collimator, and has a maximum field of about one degree or so. With a half angle larger than 10 degrees, the astigmatism and field curvature correction becomes important. A lens that has both of these aberrations corrected is called an Anastigmat lens.
Although we’ve started some lens design in the previous chapter, this is a more practical camera or imaging lens design.
Bear with me as we go through the rest of the aberrations, the spreadsheets are minimal for now.
Astigmatism
Astigmatism is a difficult concept to understand, perhaps more than coma, for some people.
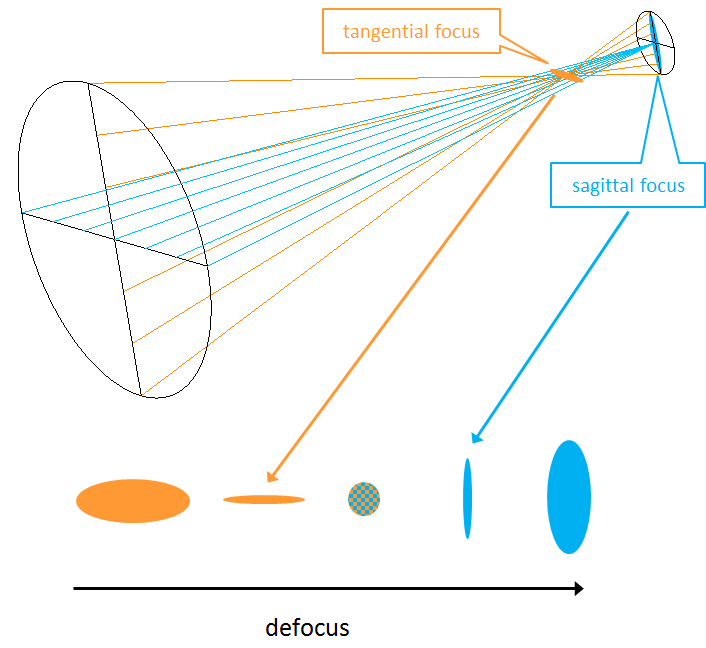
As you can see in the diagram, the point of focus is different in the two planes, the tangential and the sagittal.
The front defocus and the back defocus differs so much that the out of focus or bokeh becomes very unpleasant to the eye, especially the back focus. For cinematic lenses, the astigmatism is almost always corrected more so than typical camera lenses.
The causes of astigmatism is the change in refractive power between the two planes, since a pencil of rays at an angle pass through a different portion of the lens in the meridional and the sagittal planes. On the optical axis, the lens is rotationally symmetric, so the pencil of rays are all in the meridional plane, and astigmatism does not occur.
A simple but effective schematic and concise description on astigmatism can be found in the Astrophysics section in Hyper Physics website for Georgia State University.
I like the word Anastigmat. It is a double negative because astigmatism itself is a negative term because of the “a”. “Ana” means it is a non-astigmatic lens.
Field curvature and the Petzval sum
The field curvature is shown in the image below.
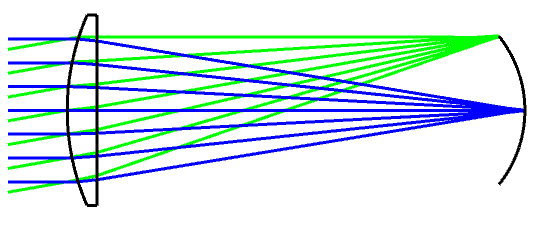
The image plane is not on a singular plane, and the image plane is curved, hence the name. That means that with a lens that has field curvature, if the lens is focused at the center of the image, the corners of the image are out of focus, and vice versa.
Conversely to astigmatism, the front and back out of focus are the same, as they are circular. Although the spherical aberration is also a circular defocus, it does not change from the center of the picture to the outer corner edges.
As far as the cause of field curvature, for a positive lens, the focus point off axis is closer to the lens than the focus point of the optical axis. This is expressed mathematically with the Petzval sum.
A Viennese mathematician Joseph Petzval discovered this phenomenon in 1843. For a thin single lens the equation is simplified to
$$
P_z = \phi_1/n_1 + \phi_2/n_2 +… \phi_k/n_k \\
\phi_t = y_1 \phi_1 + y_2 \phi_2 +… y_k \phi_k
$$
Where PZ is the Petzval sum, \(\phi_i\) is the power of each surface, and n is the index of refraction, \(\phi_t\) is the total power, and _y is the ray height at each surface. What this means, conceptually, is that the Petzval sum is decided by the power of the lenses and their index of refraction.
Historically, the Petzval sum is given as a number when the focal length of the lens is normalized to 1. The Petzval sum is said to represent the curvature of the field in the paraxial domain.
The revolutionary lens that Petzval designed, which is immortalized as the Petzval lens, ironically does not satisfy the Petzval condition. In fact, it is a very good example of a lens that does not satisfy the Petzval condition. But imperfect optics is not always a bad thing, and this lens was sought out for portraiture. It has recently been revived in the form of the Lomography New Petzval 85 Art Lens, which I think is very interesting as a lens designer.
Since the Petzval sum only contains the index of refraction n and the focal length f (or optical power \(\phi\)). The usual “lens bending” isn’t as trivial to apply.
To correct the field curvature, we can…
1) place the positive crown lens and the negative flint lens farther away from each other. If the positive lens and the negative lens are farther away from each other, the y value in the above equation is smaller, thus if the total power \(\phi_t\) is normalized to 1, that means that the power of the negative lens can be smaller to achieve the same total power, and then the Petzval sum is smaller. For Aplanatic lenses that we’ve looked at so far, the doublet lenses make this correction difficult.
2) Judging by PZ in the equation above, the other method is to decrease the index of refraction of the positive lens, and increase the index of refraction of the negative lens. This is possible for an Anastigmat, but it is the direct opposite of the colour correction and spherical aberration correction that we apply by using the high index, high dispersion lens for the negative flint lens for an Aplanat. Which is to say that a doublet lens has more field curvature than a singlet lens. For the Aplanat lenses we’ve looked at so far, this is in direct conflict with our design concept.
Distortion and transverse chromatic aberration, correction
Distortion and symmetry
So far, we’ve looked at:
1) Aplanats, which need spherical aberration, coma, and longitudinal chromatic aberration correction. This can be done with one positive lens and one negative lens.
2) Anastigmats, which correct the astigmatism and field curvature. To correct astigmatism, the lens and stop must be farther from each other. To correct the field curvature / Petzval sum, the positive lens and the negative lens need to be farther away from each other. Both are not possible with the telescope objective doublet lens we’ve looked at so far.
To summarize, to have a well corrected lens that has a field of view, we now know that there needs to be some thickness along the optical axis, compared to the entire length of the optical system.
Now, we’ll look into a lens system that is symmetric, which is important for distortion and transverse chromatic aberration.
Distortion
Distortion has two major forms, called barrel distortion and pincushion distortion.
It is best explained with a lattice like structure that looks like a barrel or looks like a pincushion, hence their names.
There are some distinct differences between the properties of distortion compared to other aberrations.
- Spherical aberration, coma, astigmatism, field curvature all make the object out of focus in the image plane. However, distortion has nothing to do with an image being out of focus.
- All of the other aberrations improve their performance with a smaller stop, or a darker F-number. However, distortion is an aberration that does not improve with stopping down a lens.
- The distortion does not affect lines that are parallel to the direction of the field.
A bit of history about distortion, in old cinematography, the best cine lenses still had some measure of distortion, especially for wide angle lenses. A lot of scenes where the main protagonist walks away down a straight path had to be shot parallel to the field.
Also, some scenes had benches, for example, that were bent the opposite way from the distortion so that the image would be straight.
$$
y = f \tan{\theta}
$$
is the equation that does not have distortion. Distortion is when the ideal height of the image is located in a different place on the image plane.
$$
(y’-y)/y \times 100
$$
(when representing in percent)
So why does distortion occur?
If a positive lens is located before the stop, the positive lens refracts the marginal ray more than an ideal lens would, so y’ is larger than the ideal y.
If there is a lens that is e away from the stop, with a power \(\phi\), think of the stop as the center of a scale, a positive lens as a weight, and the negative lens as a balloon. If the scale tips to the left, the distortion is positive and therefore pincushion shaped, and the opposite is the barrel distortion.
Higher orders of aberration affect this qualitative thought process, but the idea holds true for most cases. Therefore it is easy to imagine that symmetric systems like the Double Gauss lens has small distortion, a telephoto Iens has pincushion distortion, and wide angle retrofocus lenses have barrel distortion.
Finding a suitable value for distortion is tricky because depending on the optical system, there are different requirements. Portraiture usually blurs the background, so unless there is extreme distortion like you’re looking through a peephole, it’s hard to notice.
Landscape photographs or distance metering devices require high distortion correction, if objects such as railways need to be imaged in a straight line.
Also for photographs, even if the absolute value of distortion is small, a non-smooth transition of the distortion can look very unpleasant to the eye. In this case, not only is the absolute value of the distortion cared for, but the change in distortion also needs to be taken into account.
Of course, a lot of digital cameras have software distortion manipulation, so all of this may be moot. But it’s important to figure out whether or not the system requires an optical distortion correction or not, and what the restrictions are.
Transverse chromatic aberration
If the optical system has a positive lens after the stop, after the marginal rays pass the lens, the shorter the wavelength is, the more it is refracted towards the image plane. The index of refraction for shorter wavelengths is larger in the material. This effect is the transverse chromatic aberration.
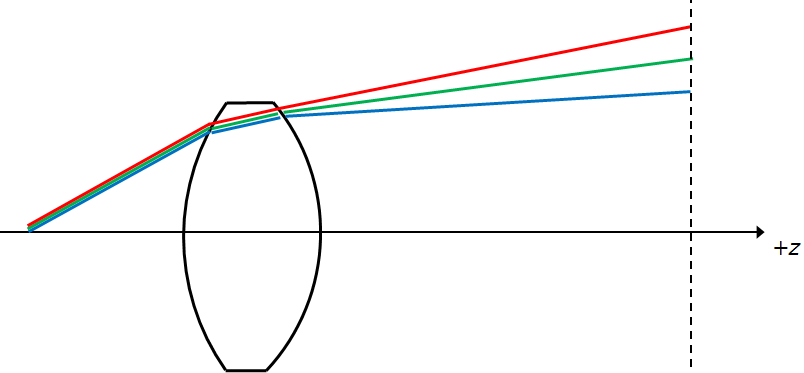
If we are photographing on a plane, we would see the transverse chromatic aberration most clearly at the edges.
Not to be confused, the lens may have longitudinal chromatic aberration as well, at a point off-axis.
Similarly to distortion, the correction of transverse chromatic aberration can be done by making the optical system symmetric with the stop in the center. The amount of refraction in the rays depending on the wavelength are balanced.
Expressed in an equation, the transverse chromatic aberration is
$$
T_{ch} = \sum_{i=1}^k y_{m_i} \times y_{p_i} \times \phi_i / \nu_i
$$
Where ym is marginal ray height, yp is the chief ray height, \(\phi_i\) is the power, and \(\nu_i\) is the Abbe number of each surface.
While the longitudinal chromatic aberration was
$$
L_{ch} = \sum_{i=1}^k y_{m_i}^2 \times \phi_i / \nu_i
$$
In summary, the longitudinal chromatic aberration is corrected with a positive lens and a negative lens, while the transverse chromatic aberration can be corrected with positive lenses only if they are placed symmetrically from the stop.
Raytracing, Ray diagram, Aberration diagram
The importance of ray tracing
Optical lens design is founded on ray tracing. We can discuss OTF (Optical Transfer Function) and wavefront aberrations, but very often raytracing is at the core of the design.
We humans are inherently good at recognizing patterns, much more than computers. Therefore, an expert lens designer using a relatively primitive computer can usually provide a better lens design than a novice optical lens designer using a supercomputer. Pattern recognition for lens design includes the cross-sectional diagram of the lens, the ray path diagrams, and the aberration diagrams. Rather than go into the theory, let’s take a look at some examples.
I don’t see many cases where people share their knowledge for actual ray tracing techniques. Certainly computer programs do it for us now, and understanding the process can help our lens design process many fold.
Ray trace initialization: a triplet lens example
We’ll do the actual lens design below, but let’s take a look at a triplet lens for raytracing.
For the images, I am using the optical design software Zemax , but i haven’t found a good illustration software that handles the drawing of lenses well. I’ve done them by hand in the past to get a feel for the drawing process, but even drawing them in software can be beneficial.
1) Wavelength
For photographic lens design, the d line and the g line are enough for a rough design. For a triplet, three wavelengths are sufficient. For telephoto lenses and large focal length range zoom lenses however, four wavelengths d, g, F, C are needed. Some cases use five wavelengths, including IR.
2) On-axis rays
For a rough design, the marginal rays and the paraxial rays are sufficient. The next step in the rough design utilizes the marginal rays and the 1/sqrt(2) of the marginal ray, or about 70% of the aperture. Although we will not go deep into this, for modern faster F-number lenses like F1.0 and F0.95, the larger aperture causes higher orders of spherical aberration, so looking at the 50% field and 90% of the aperture is good practice.
3) Field of View (FOV)
Usually, the 100% highest field, the middle 70% field, and the relatively small 50% field, and the optical axis 0% field is traced. In our current example, we have an angle of 23.17 degrees for the largest field that has a tangent of -0.428, when the object distance is at infinity. As we will see later, this corresponds to the diagonal position of 21.63mm from the center of the image, which is half the diagonal for a 24mm x 36mm image size, which is the size of a 36mm, or full-frame, or 135 format film (or sensor) size, for a 50mm focal length lens.
4) Number of rays to trace per field
Off-axis, the rays in the meridional plane are non-symmetric from the center, two both sides are taken at 70% and 50% aperture and 7 rays are traced (-100%, -70%, -50%, 0%, +50%, +70%, +100%). The sagittal rays are symmetric, so 3 rays suffice (100%, 70%, 50%).
Triplet lens design
The complete lens
I think the triplet is the perfect lens to explore lens design. Although it is not the first photographic lens designed, almost all modern lenses can be traced back to the triplet. Therefore, studying the triplet carefully can provide the basis for most modern photographic lens design. Let’s design the triplet together.
But first, let’s review the lenses we’ve spoken of so far.
One positive lens, with the stop located on the surface

- The stop on the surface and the 1:-6 radius ratio gives us the smallest possible spherical aberration. Third order coma is also close to zero.
- Longitudinal aberration cannot be corrected because there is no negative lens.
- The stop on the surface also prevents transverse chromatic aberration and distortion.
- Astigmatism can’t be corrected because only one lens power governs the total power of the lens.
- Likewise for the Petzval sum, i.e. the field curvature, cannot be corrected.
Landscape lens, with the stop in front of the lens
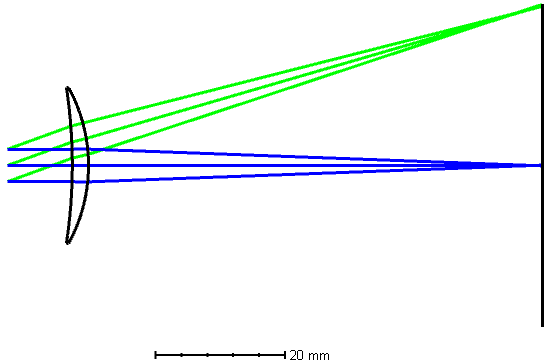
- The positive lens and the stop is separated, and the meniscus lens corrects the astigmatism and coma.
- However, the spherical aberration is completely out of whack, and the only way to minimize it is to make the aperture smaller.
- The distortion can’t be corrected because of the asymmetry about the stop.
Telescope objective cemented doublet

- The spherical aberration can be corrected to zero at the marginal ray.
- The chromatic aberration and the coma can be corrected.
- However, the Petzval sum is larger than a single positive lens. This is not critical for a small field system like a telescope, but we need to recognize those limitations.
Telescope objective separated doublet

By splitting the lens, the spherical aberration, longitudinal chromatic aberration, coma, field curvature can be corrected, but the lack of symmetry about the stop means that the distortion can’t be corrected.
Just like that, we can now qualitatively and conceptually dissect the lens and figure out the expected performance without opening any software. This prevents blindly optimizing a non-winning design concept, by tackling lens design without knowledge and just the software.
Now, onto our triplet. How are we going to rectify the problems above and make a compete lens that corrects all of the seven deadly aberrations?

Take the separated telescope objective and split the positive lens, put it at the end, and make it a triplet.
- The negative and positive lens combo at the end can correct the longitudinal chromatic aberration.
- There is sufficient symmetry so that distortion and transverse chromatic aberration can be corrected.
- The negative and positive lens combo are separated, so the Petzval sum and therefore the field curvature can be corrected.
- Spherical aberration, coma, and astigmatism, can all be corrected due to the degrees of freedom with the 3 lens bending.
So, the monochromatic third order aberrations and the two chromatic aberrations can all be corrected, and we finally have an example that has a reasonable field of view and relatively fast F-number as well.
The triplet later can evolve to an Ernostar type, which leads to a Sonnar type. The triplet can also evolve into the Tessar type, and most notably the Double Gauss type.
The triplet at its simplest form does not take thick lenses into account, and can be designed with thin lenses. This allows for lens bending that is sufficiently correct, and the lack of cemented surfaces make the triplet a very good tool for learning lens design.
H. D. Taylor wrote a patent in 1893 (GB 22,607), a paper in 1909, and wrote the book “A system of applied optics” on the triplet. Max Berek, A.E. Conrady, B.K. Johnson, Robert E. Hopkins, Rudolf Kingslake, Fumio Kondo, all giants in lens design, have written about their methods for improving the triplet design. Even though classified as a triplet, in their examples there are some highly asymmetrical types, large aperture types, with all kinds of variations. But for now, let’s stick with the standard type of triplet.
Thin lenses and 3rd order aberrations
As we’ve discussed before, 3rd order aberrations with lenses without thickness, is thin lens 3rd order aberration theory.
This can only be solved iteratively, and this can be applied to more compact lenses and zoom lenses albeit partially, and is very useful. We’ll use it here with the triplet design as well.
Also, we can divide the properties of the lens into the lens bending portion of the element, and the power portion of the element. Lens bending does not affect the power of the lens, so they can be evaluated and corrected separately.
Lens bending corrects one set of aberrations, and the power of the lens corrects a different set of aberrations, so we can see the properties of the lens clearly. We’ll definitely look into this for the triplet, but for zoom systems that can be regressed to thin lenses in groups, this is also useful.
One more thing, optimization using a computer is almost a brute force approach, while thinking about the 3rd order aberrations and the thin lens equations is a more artisanal approach, looking through the system properties and figuring out the uniqueness of our design.
Looking at the cross sectional diagram and the ray diagram, using our pattern recognition and intuition as human beings can be a very powerful lens design process. Optimization with a computer is also powerful, but in a different way.
Triplet design steps
Step 1. Choose your glass
Glass. The biggest choice in lens design. Even for a relatively simple lens like the telescope objective, we needed to choose the glass carefully. For a triplet, with just one more lens, it becomes critical.
The danger in using the computer optimization for glass selection has to do mostly with the price if the lens, where it will choose the lens based on it giving the best answer as the merit function decreases to a minimum. If you’re like me when I was starting out in lens design, you would have made the index of refraction and the Abbe number variable parameters, and you would have blindly optimized the system. Then you would have gotten a material that has an index of refraction of say, 2.40 and a Abbe number with three digits. But you aren’t like me.
I’ve recently noticed in Zemax there are ways to use the global optimization and the “substitute” feature to choose different glasses in the lens catalog to optimize performance, and can even choose the range of index of refraction, if the glass is obsolete, and the price if the information is in the lens catalog.
However, we can face some problems in choosing glass automatically. The aforementioned cost is one. Density, therefore the weight of the lens, making it heavier AND more expensive is another. Some lenses have absorption in the blue spectrum which is manageable if the lens is relatively thin, but makes the image yellow if it is too thick. Other lenses are soft and scratch easily, therefore are not suitable for the front most lens, like in the Leitz Summar lens. Some lenses have a lower melting point (Tg) and hard coating is difficult. Glass that cracks when polishing. Glass that expands more with temperature, compared to other glasses. This is just to name a few, and we can’t account for all of these in the optimization software.
Choosing the glass “ranks” the triplet, meaning the choice of glass has a direct impact to the optical performance.
There are many lenses to choose from for the crown lens, but the choice of the lenses determines the Petzval sum, so making a mistake here will cost us dearly as we go forward.
The glass SK16 (n = 1.62041), for a lens system with F4.5, gives a Petzval sum of about 0.35, LaK8 (n = 1.7865) can make a F3.5 to F2.8 lens about 0.25 to 0.3, so a higher index of refraction allows for a smaller Petzval sum, and the possibility of a faster lens with larger aperture. Usually, if the positive lens has a higher index of refraction, the negative lens will also have a higher index of refraction. This allows the spherical aberration, coma, astigmatism, to be corrected as well.
Once the positive lens is chosen, we choose the negative lens, but the Petzval sum is calculated much later in the process. That means we have to use our experience or experience from others to choose wisely at this stage. Not only is the “rank” of the triplet decided here, but also the form of the triplet as well. There are many different shapes or “forms” within the “triplet” family, but the index of refraction choices determines the form.
For example, this is Taylor’s triplet lens, from the patent GB 22,607. If we look closely at the glass we would see amazing performance for the glass Taylor could use.
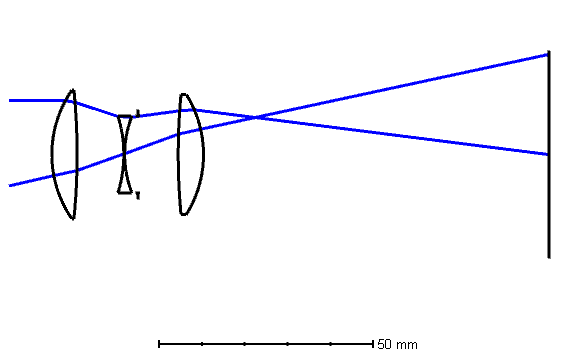
This is a triplet with an F-number of 1.9 (US2503751). A creative choice of glass is chosen, and significant optical poser is needed for the two positive lenses.
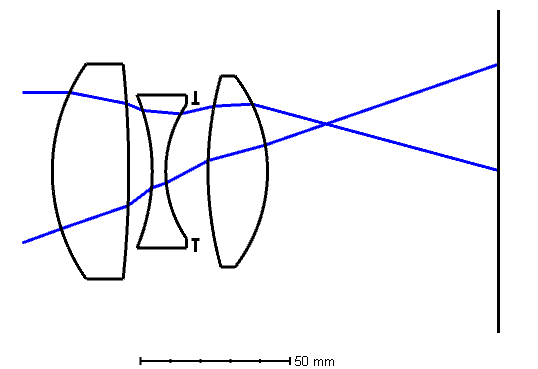
This is a triplet with wide FOV (US3418039). Interesting that the index of refraction is almost the same for all three lenses.
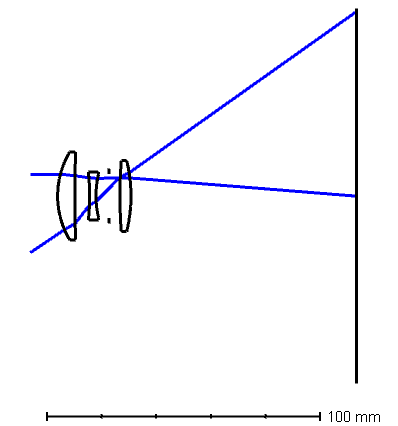
This is a triplet that is color corrected extremely well (US3486805). If we look at the patent, we’ll see that glasses chosen are very exotic, and have extremely low dispersion, with Abbe numbers like 95.
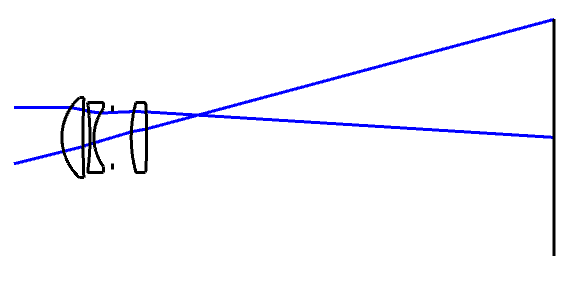
At this stage, we need to choose a negative lens, go forward, and if things don’t go well, we choose the glass again. This makes lens design difficult, and even the merit function of the optimization software can’t fully account for this unless something is added to the process to jump out of a local minimum in the optimization.
Looking at different glass would be a lot of fun. But let’s not get too carried away yet. We will design a relatively normal system, so for our example, we’ll choose SK16 of the positive lenses, and F4 for the negative lens.

Step 2. Schwarzschild solution
At this point, choosing the glass looks like a random process. It is true that without doing a few triplet designs, we can’t know that these glass choices make the Petzval sum and astigmatism manageable in the future steps.
It may be obvious that we’ve chosen a combination that works well in practice. Back in school, I heard the phrase “we will use numbers that we know will work” a lot, and this is a typical response. Let’s at least take a closer look at our choice of glass without completely dismissing it as “well, it just works”.
- The longitudinal chromatic aberration:
If the spherical aberration does not have a huge chromatic component, it is manageable, but this is not apparent until step 5. The amount also changes with the F-number of the lens, and the wavelength range of the optical system as well. We have no other way than to reference any designs we’ve done in the past, or designs we see in patents. -
The Petzval sum:
If we can make the Petzval sum small we can design a lens that has a larger field of view, but since each lens power increases, it is difficult to design a large aperture lens. The amount of aperture we can afford depends on the index of refraction of the glass. A high index glass allows for larger aperture, because the spherical aberrations are smaller due to the larger radius of curvature with respect to the lens power. On the other hand, a large aperture lens has shallower depth of field, so the field curvature (and hence the Petzval sum) must be small. If the field of view is small, the Petzval sum can be large, and larger apertures are possible.
In any case, the Schwarzschild solution is a method derived by Karl Schwarzschild, a German physicist and astronomer. At the time, he felt Germans were a step behind the English as far as optics went.
We set a fixed focal length, and correct the longitudinal chromatic aberration, and construct three equations for the Petzval sum, and solve for the three values of power. The three equations are total power, Petzval sum, and longitudinal chromatic aberration.
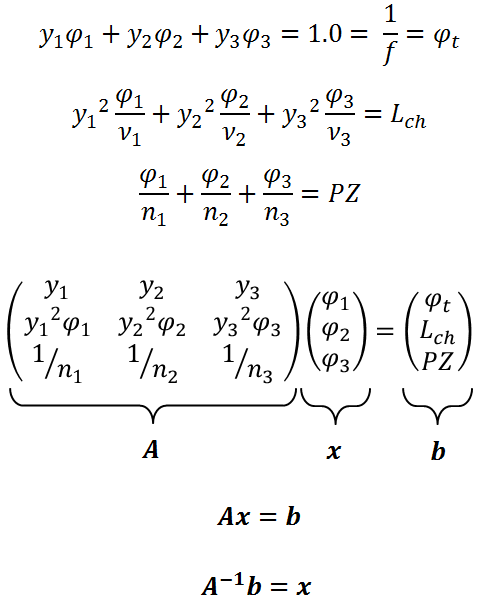
So this makes our matrix, which is solvable for the lens power \(\phi_1\), \(\phi_2\), and \(\phi_3\) in matrix form by using the inverse of the matrix A.
This sort of solution is quite simple for the modern computer. I’ve used a matrix solution based on the system of linear equations in Excel, the code MINVERSE(matrixA) to get to this solution.

Further, the distance between the lenses are calculated as in step 2(c).
This is a useful method for choosing the position and the power of the relay lens for a zoom lens as well.
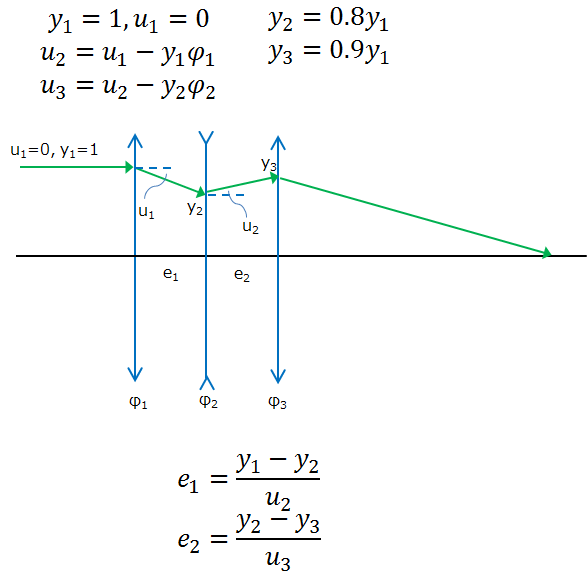
The only issue here is how to choose y2 and y3, namely the height of the marginal ray at the second and third lenses.
- y3: If this is larger e2 is larger. Which means that the negative lens moves closer to the front. The opposite is true for the opposite case. Usually, e1 is larger than e2, with a ratio of 1.05 to 2.00 or thereabouts. The farther away from 1.00 the ratio is, the larger field of view is possible.
Usually, a normal field of view, a slightly longer e1 compared to e2, or a slightly shorter e1 compared to e2 is preferred. If e2 is larger, the stop can be placed in between the negative lens and the last lens, and the back focal length can be longer, giving more room for the lens barrel.
This becomes is clearer in step 3, when we look into the 3rd order thin lens aberrations.
- y2: When this is small, \(\phi_1\) and \(\phi_3\) ratio changes, and \(\phi_3\) is larger. The marginal rays change as a product of yi and \(\phi_i\), and if \(\phi_3\) is larger than \(\phi_1\) it is easier to correct the aberrations.
- There are times that whatever number we choose, we only get an extremely long triplet lens, or a triplet lens with a ratio of e1 and e2 that is extremely different. In this case, it is best to choose different glass, or to choose a different Petzval sum. In other words, this is where we see whether our glass choices were correct, and our Petzval sum was adequate in the previous step.
Step 3. Correct thin lens 3rd order aberrations
- Use the 3 degrees of freedom that we have, and correct 3 aberrations.
Namely, this is the spherical aberration, coma, and astigmatism. The 3 degrees of freedom are the lens bending of the three lenses.
3 lens powers, 2 lens distances, are another set of degrees of freedom. We use these to set the focal length, the longitudinal chromatic aberration, the Petzval sum, the total thickness, and the ratio of the lens separation. The three lens bending does not change the focal length, the longitudinal chromatic aberration, the Petzval sum, the total thickness, and the lens separation ratio.
From the symmetry of the system, the lateral chromatic aberration, and the distortion (we will assume is good enough for now due to the symmetry, and is corrected enough at this point to be able to go forward with the lens design.
Therefore, the triplet is the first lens we’ve encountered that can correct the 5 monochromatic 3rd order aberrations and the 2 chromatic aberrations.
- Starting point lens shape
The first lens we will use the smallest possible spherical aberration shape, R1/R2 = 1/(-6), and the third lens as the opposite shape, R5/R6 = 20/(-1). The negative lens we will start off as a double concave lens.
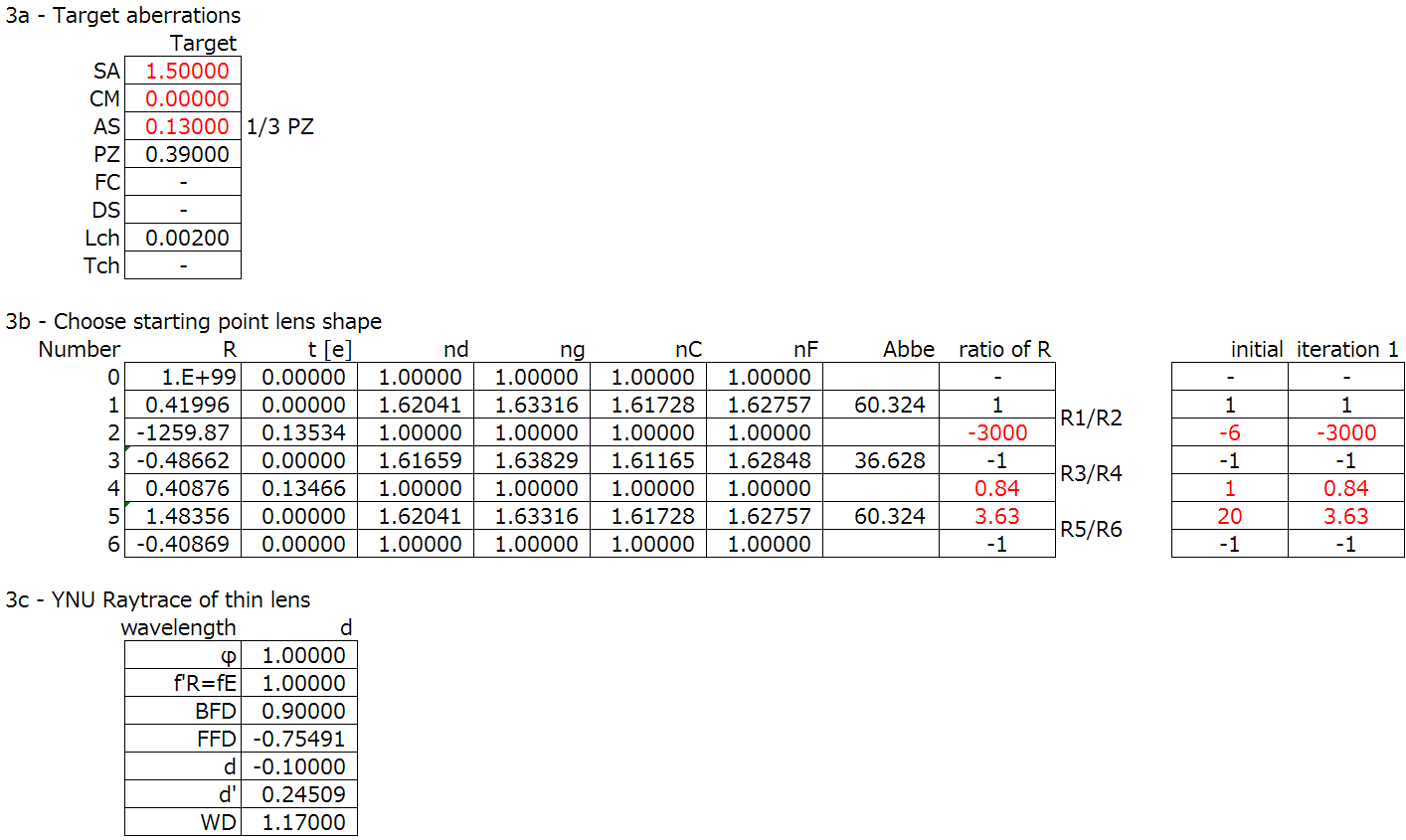
The symmetry of the system allows for correction of the off-axis aberrations. The first lens is larger than the third lens and can correct the spherical aberration the most effectively. As a side note, this is true for most lens types except for retrofocus lenses.
- Target aberration values
We choose: - SA = 1.5 ~ 2.0
- CM = 0 (coma)
- AS = -1/3 PZ
Where SA is spherical aberration, CM is coma, AS is astigmatism, and PZ is the Petzval sum.
The non-zero spherical aberration is to balance the 5th order spherical aberration. Whether or not this assumption proves true or not is found by calculating the 5th order aberration or using ray tracing analysis. At this point, we make this assumption, correct the lower order aberrations, calculate a better target value in the next step, change the assumption in this step and repeat. Not easy, for sure.
- Aberration correction
Each lens affects the aberration differently, and by changing the lenses we can get a feel for each.
The last lens is the dominant astigmatism corrector. The first lens is the dominant coma corrector. The middle negative lens is the dominant spherical aberration corrector. Think about them in this way and the optimization becomes easier.
A more thorough analysis of the correction can be done.
- Since we assume the stop is fixed to the negative lens, we know that the lens bending of this surface does not change the astigmatism. For this lens, the spherical aberration and the coma are the only aberrations controllable with lens bending.
-
If the first and third lenses are bended as meniscus lenses with the convex side facing the stop, the astigmatism is negative.
-
The coma is the opposite, and although the first lens like the meniscus mentioned above causes the coma to go in the plus direction, the third lens meniscus causes the coma to go in the minus direction. Using this property we can keep the astigmatism uniform while changing the coma, and correct the spherical aberration by bending the negative lens. Of course the negative lens changes the coma, but we can account for it and correct it simultaneously.
I have played around with the numbers myself, and tried to get within the target range as best I could.
I have R1 = 0.420mm, R2 = -1260mm, R3 = -0.487mm, R4 = 0.409mm, R5 = 1.484mm, R6 = -0.409mm in step 3(b). But look closely at “iteration 1” at the left. I have controlled the radius of curvature by setting the ratio of R1/R2 = 1/(-3000), R3/R4 = -1/0.84, R5/R6 = 3.63/(-1). I made sure that in my spreadsheet, the ratio of the radius changes, but the power of the lens does not. I use the power values from 2(c).
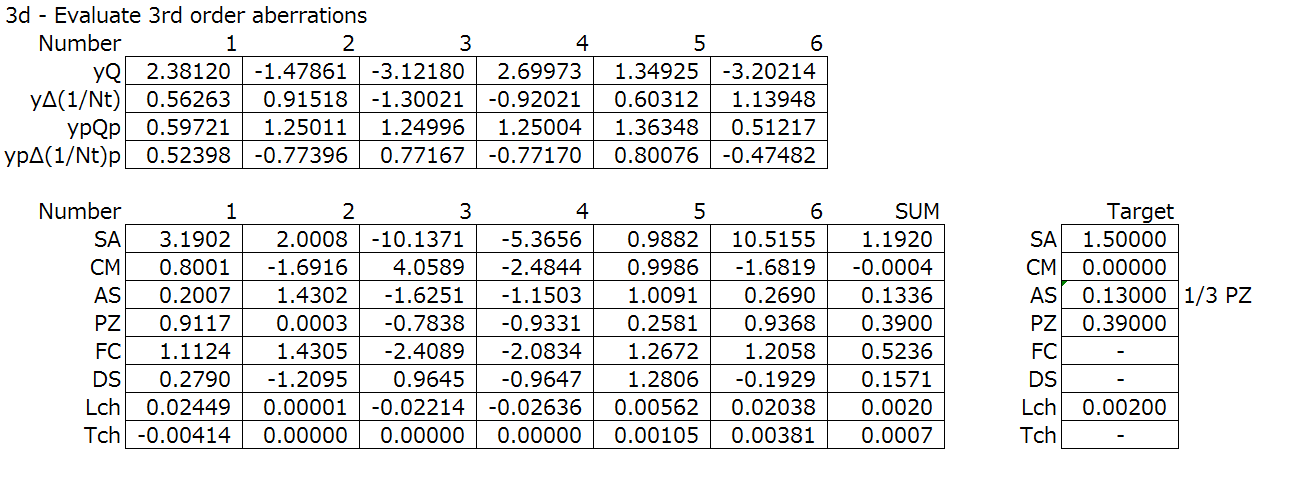
At this point, the lens is still a thin lens, with only the separation between the lenses defined. We have a thin lens system with the stop fixed on the lens surface. Let’s take a look at the how to observe the properties of a thin lens system.
The lens properties are calculated, like the focal length of three lenses, their separation, and the radius of curvature of the surfaces and their ratios, so that means that the lens bending is decided. Also, the three lenses have an index of refraction and Abbe number, so the type of glass is also decided.
With this information, we can calculate the principal points, the overall focal length, and the back focus of our triplet.
By applying the paraxial ray tracing and paraxial marginal ray tracing we can calculate the height of each lens from the rays, and the ray angle with the optical axis.
In addition, the 3rd order aberrations for each surface are calculated, and the sum is given for the overall 3rd order aberrations.
For the spherical aberration, coma, astigmatism, Petzval curvature, and longitudinal chromatic aberration, we can see that the one negative lens counteracts the aberration generated by the two positive lenses.
The distortion and the lateral chromatic aberration is not generated by the negative lens because the thin lens is fixed with the stop. The balance is achieved by counteracting the aberration from each positive lens by placing them about the stop, and generating aberrations of opposite sign.
This means that the distortion and the lateral chromatic aberration is dependent on the distance of the stop to the surface with power, as we discussed before.
The negative lens is fixed with the stop, so the astigmatism is not dependent on the lens bending, and only dependent on the power.
The first lens has more power than the third lens, and although the first lens has almost the smallest spherical aberration possible, the third lens is the opposite shape and is not that much larger.
The two positive lenses have to be this shape in order to maintain the symmetry needed in the system. Without this symmetry the astigmatism cannot be corrected for larger angles in the field of view. Therefore, with the object at infinity, the parallel ray focusing to one point, is a property of an Anastigmat. Even in a Double Gauss, the lens in the very front is not all that different from the spherical aberration 1:-6 theorem, and the last lens is also the same in an opposite shape. Same with the Tessar as well.
In summary, now that we know how the lens system works, it is very advantageous in optimization. We can already see that this is a much smarter approach than just punching the numbers in a computer and clicking “optimize”. (Recommended reading: H. H. Emsley’s “Aberrations of thin lenses”)
What to do if we can’t find a solution
However, there are two possible design scenarios we might face.
- We might have a case where the aberrations cannot be balanced, or corrected.
- We might arrive at a solution where the overall 3rd order aberrations have hit the target values, but the aberrations on each lens surface is relatively large. Both cases almost guarantee that the higher order aberrations are large, and therefore it is highly likely that the lens will not have good overall performance.
In this case the only thing we can do is to go back to Step 2 and rethink the target aberrations we set earlier, or go back to Step I and perhaps choose better (read: expensive) glass and start over. Some lens designers like to start over often, while others like to iterate with trial and error at an intermediary step, and both approaches are correct and incorrect. Both the skill of being able to leave a lens design behind and the skill of persisting with a lens design are needed.
I completely understand that going back to Step 1 is a chore, but there are times when such courage is needed. On the other hand, if you go back too often, you can end up in a back-and-forth spiral of doom.
For example, you can change the index of refraction of the glass without changing the Abbe number, and the Petzval sum will change with 1/n, while the radius of curvature changes with (n-1) and has a large effect on the spherical aberration while not changing the Petzval sum too much. Of course, the focal length and chromatic aberrations do not change.
I suggest saving lens designs often and going back a step or two and compare the designs at the end. I do this for much more complex computer aided lens design as well.
Step 4. Make the lenses thick
The positive lenses require enough of an edge thickness so we can handle it, and the negative lens requires the center thickness to be large enough so that it can be fabricated.
To make the lenses thicker within the design, we keep the radius of curvature ratio of both sides of each lens intact, and keep the focal length of each lens the same as we make the lens thicker.
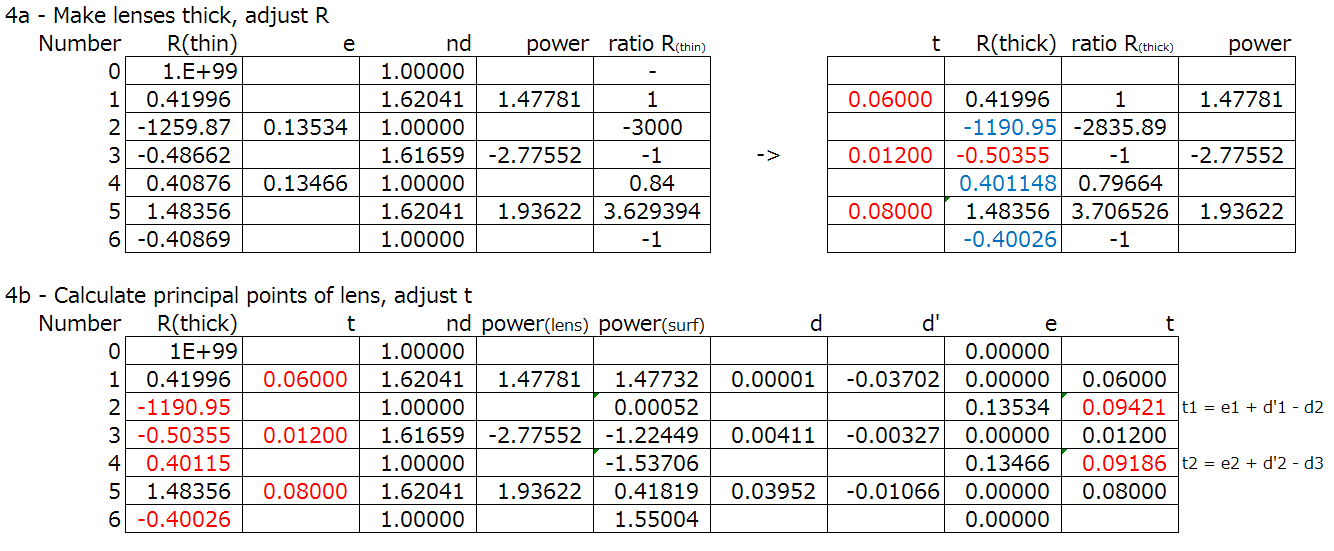
The thickness changes the focal length of the lens, so we keep our thin lens focal length by changing the lens shape, but in changing the lens shape we keep the radius of curvature ratios intact.
By doing this we also keep the separation between the principal points the same, so most everything we did in the previous step is carried forward. Of course, the thickness changes the chromatic aberration and the 3rd order aberrations from the thin lens results.
A few iterations to the target values gives us the results of the design.
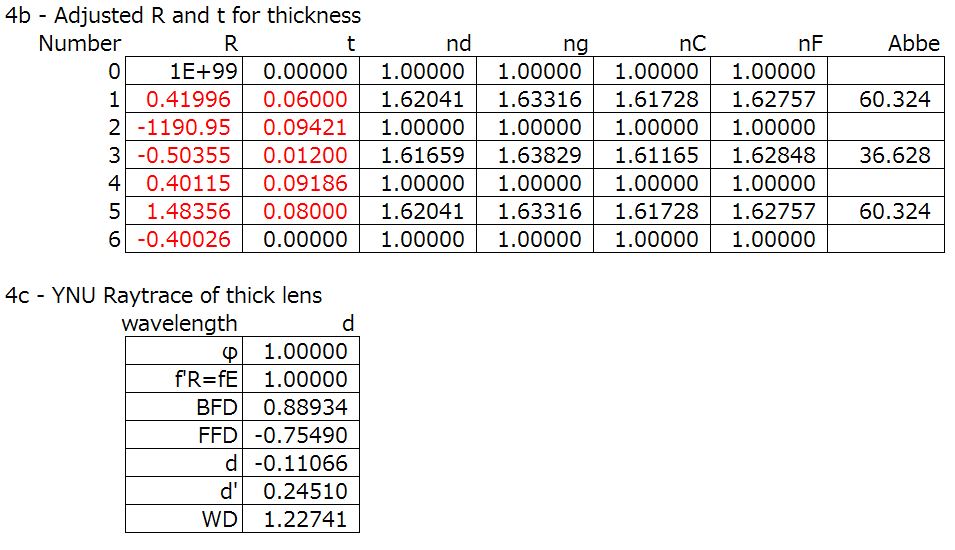
And we evaluate the third order aberrations.
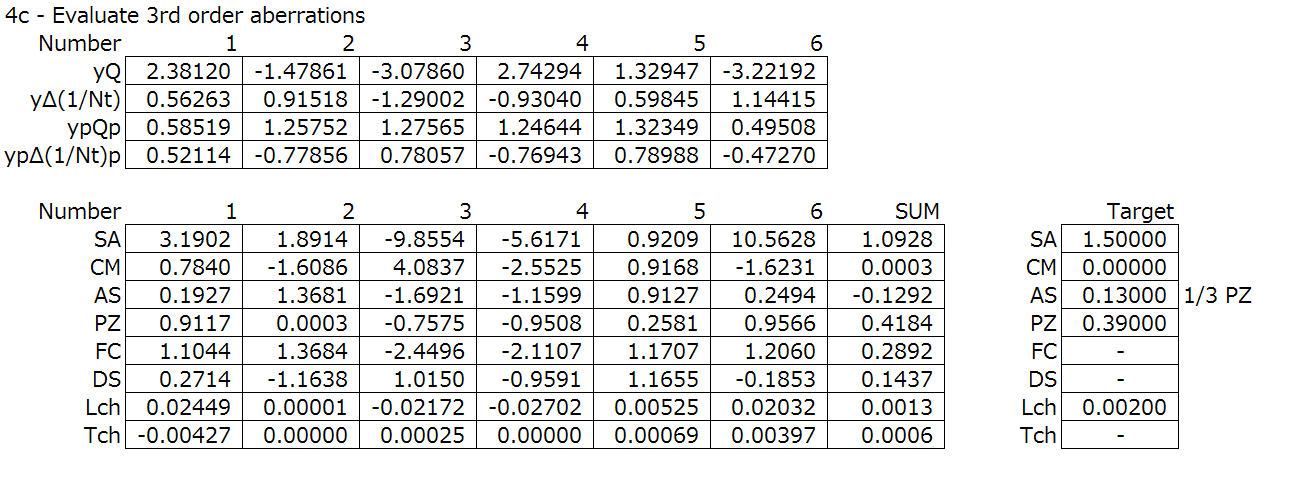
Not bad, right?
Step 5. Correct aberrations by raytrace
Although we don’t do this step with a spreadsheet, at some point, the aberration calculations from ray tracing is required to correct the aberrations more accurately.
We’ve looked at a typical lens design step by step. If you’ve read this far, you’ve seen that there are certain steps where our intuition was needed to make good design decisions, while other times there were steps where previous design experience played a role in going forward. One big step into becoming a great lens designer is the ability to understand the properties of aberrations, but another way to become a great lens designer is to simply do a lot of lens design. There are no shortcuts.
We’ve seen that lens design requires iteration, laborious effort, and the ability to make decisions. It either looks like an exciting game to solve, or a pandemonium process that can’t be explained theoretically. We decide which it is, and I prefer the former.
Final check of our Triplet lens design
I want to make two comparisons of our lens design with the classic Taylor triplet from 1893 (GB 22,607). The first is a comparison of the 3rd order aberrations with our spreadsheet, and the second is a comparison with Zemax.
Check the performance with a spreadsheet
Okay, we’ve already looked at this, but the 3rd order aberrations for our triplet lens.

This is the lens design and 3rd order aberrations for the Taylor triplet.
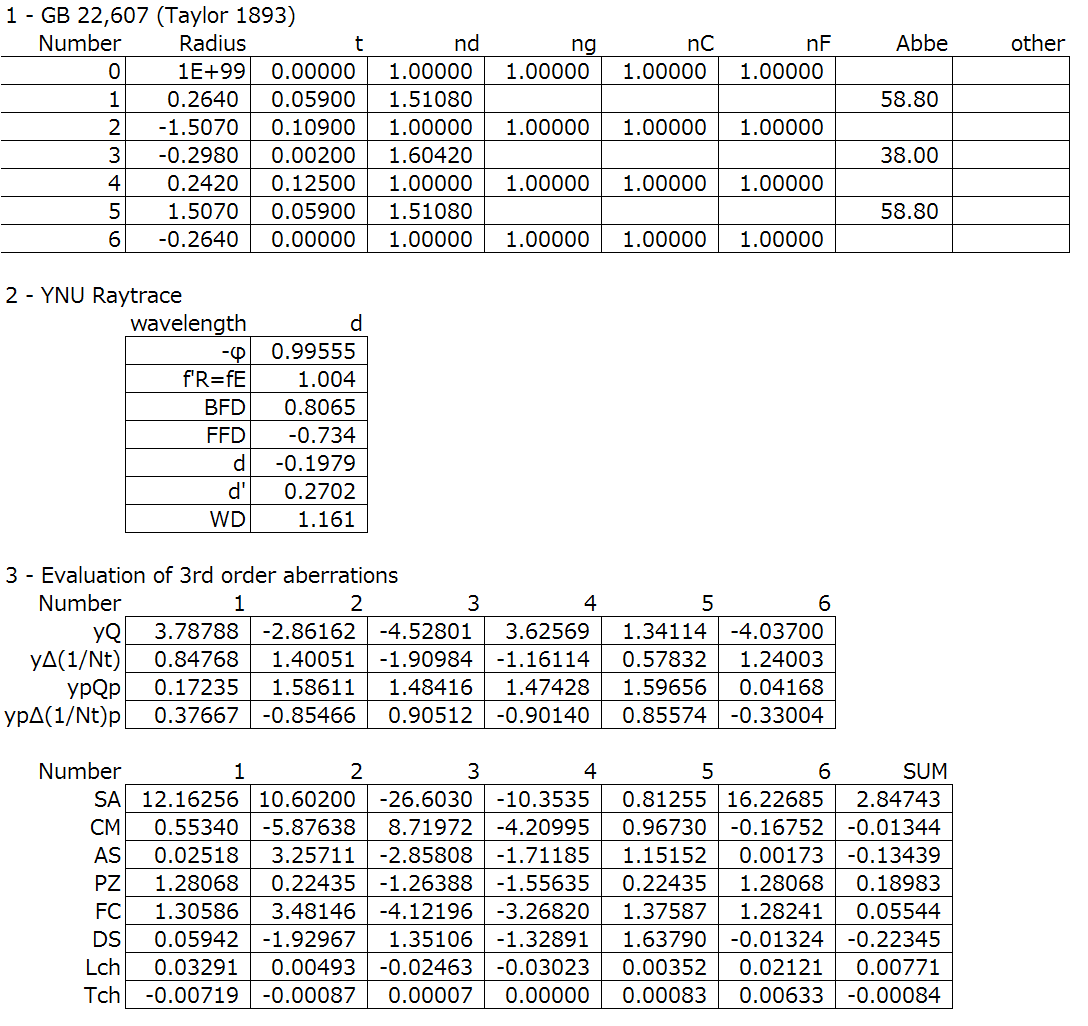
What do you see?
Spherical aberration (SA), we win.
Coma (CM) and astigmatism (AS), is essentially a tie.
Petzval radius (PZ), Taylor wins.
Distortion (DS) is about the magnitude, but notice that it is opposite.
Longitudinal chromatic aberration (Lch), we win.
Transverse chromatic aberration (Tch), is a tie.
Since we didn’t use extremely exotic glass, some aberrations are better corrected than others, and many are a tie. overall, the difference in performance between the two lens design comes down to the choices of the target value for the aberrations.
Check the performance with Zemax
Now that we’ve designed and compared our lens with a spreadsheet, let’s use some modern optical design software to check our results.
For the people that are wondering if our lens design really is good, let’s pop it into the software.
I use Zemax a lot, so that’s what we’ll use here. For other optical design software, my hope is punching in the numbers is trivial.
Other software are Code V, Oslo, and OpTaliX, among others.
The FOV is the same, the aperture is the same at F/# = 4.
Our triplet scaled to a focal length of 100mm.
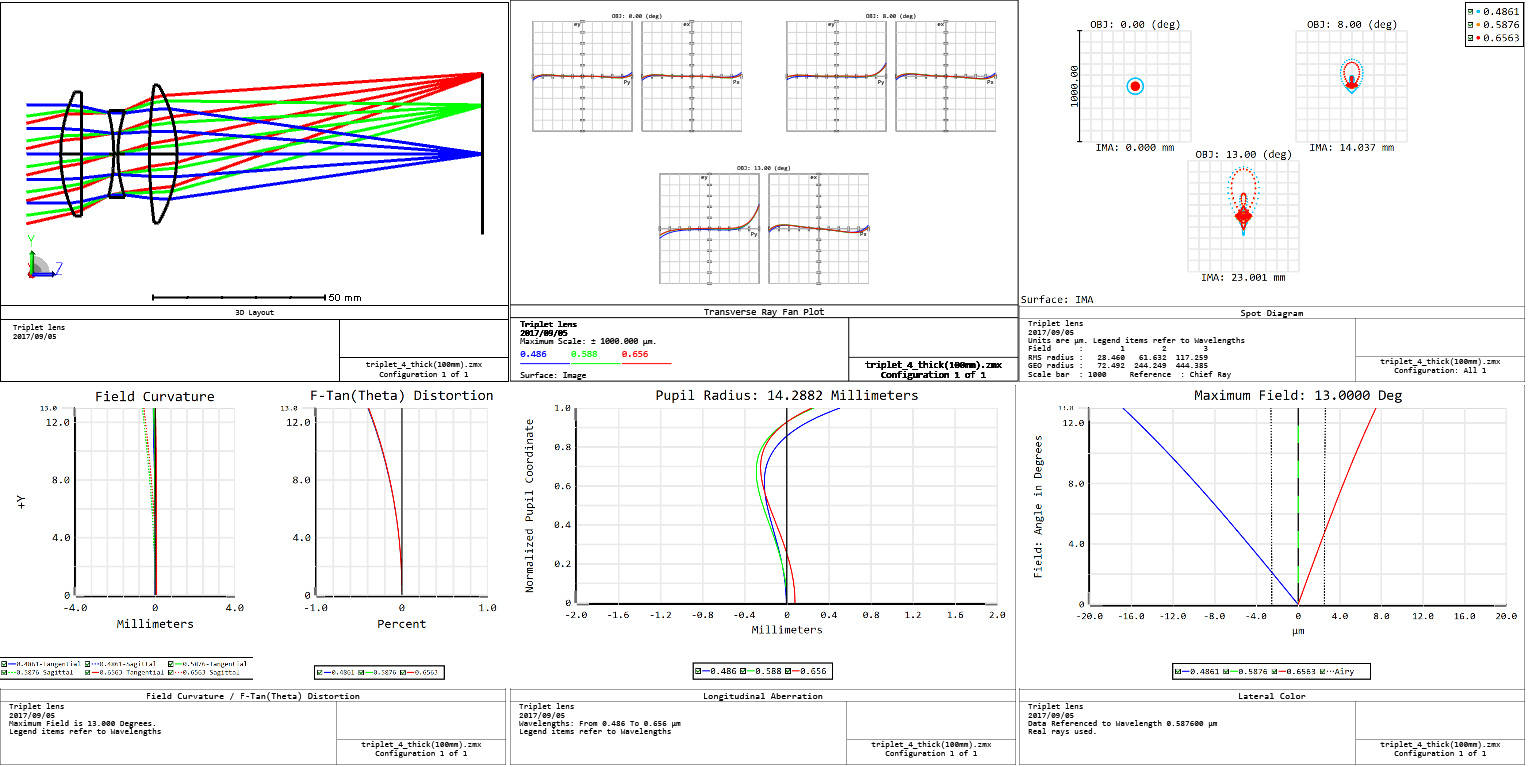
(Click to enlarge)
Taylor’s triplet scaled to a focal length of 100mm.
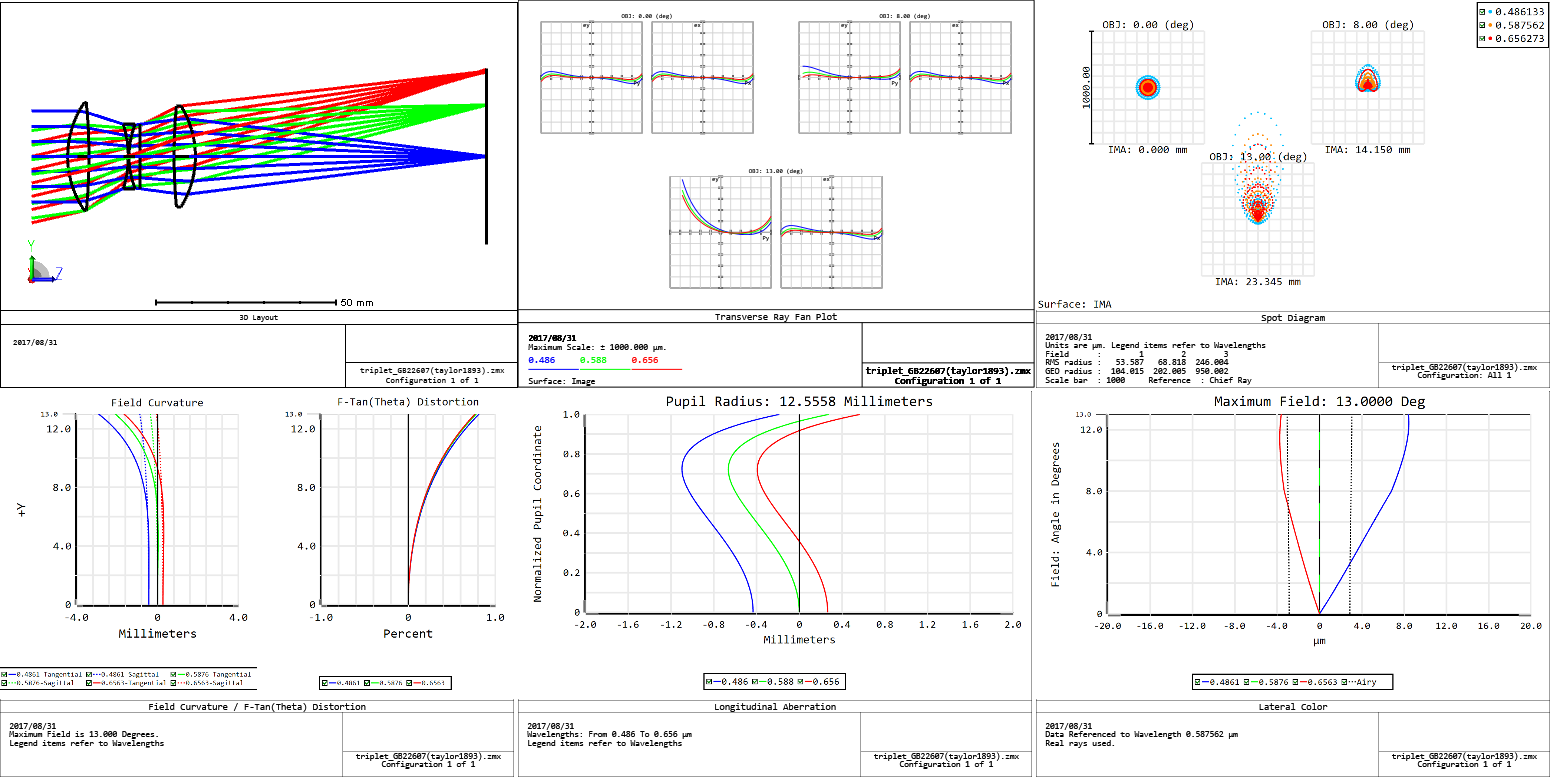
(Click to enlarge)
What do you see this time?
Our spherical aberration is better. This is most apparent in the bottom middle picture of each design (longitudinal aberration). The green line in our design doesn’t get as large at about 70%~80% of the pupil radius. We both take into account the 5th order spherical aberration and made the 3rd order spherical aberration nonzero. Notice also that the spot diagram in the top right picture, the 0deg spot is smaller for our design.
Coma difference is negligible, so it’s a tie. This is most apparent in the top right picture, the spot diagram. We can see a slight comet like shape in the higher field.
Astigmatism is comparable in the bottom left picture, the left is the field curvature and we see a small difference between the tangential and sagittal field curvature. Closer to the center Taylor wins, but for the higher fields we win.
The field curvature is very flat for smaller fields in both designs (the left graph of the bottom left picture).
The distortion is indeed opposite and about the same magnitude for both designs (the right graph of the bottom left picture).
The longitudinal chromatic aberration is the color difference in the bottom middle picture, or how close the blue, green, red lines are to each other. We win.
The transverse chromatic aberration in the bottom right picture is also opposite (the blue and red are opposite), since the distortion is opposite. It’s a tie.
Honestly and objectively, I lose overall. Look at Taylor’s patent, and you’ll see that the positive lens and negative lens are not only the same glass, but the exact same shape, just flipped in a mirror image about the stop. Taylor corrected the aberrations with a little adjustment of the negative lens, and the adjustment of the position of the positive lenses. Truly, the work of a genius.
What do you think? Do you think we did pretty well with just a spreadsheet? Do you think Taylor’s design from 100 years ago was good or bad? Do you think you could do a better job just using Zemax with the same glass? Do you think the essence of lens design is not brute force optimization in the software? Your answer and thought process will make you a better lens designer.
Final action step: Design a triplet lens with a spreadsheet.
Even better, download the spreadsheets used in this Guide!

Get Your FREE Lens Design Guide with Spreadsheets
Enter your name and email for instant access to our Guide to Classic Lens Design (in PDF format) and the actual spreadsheets used in the guide!
??100% privacy, and we hate spam. When you sign up, we'll keep you updated usually with one email per week, occasionally up to a few times a week. Unsubscribe at any time.
Other triplet forms
If you’re familiar with the history of photographic lenses, you’ve probably seen a lot of different shapes of lenses that are similar to a triplet, but different.
Some examples are the Tessar, Ernostar, Sonnar, Unar, Heliar, Protar lens, and many others.
The Ernostar
For example, the Ernostar was designed by the genius Ludwig Bertele when he worked at a camera / lens company called Ernemann, hence the name.
Taking what we’ve discussed in this guide, let’s think about the lens design principles in a qualitative way.
In 1925, Bertele added a positive lens in the front of the triplet and attempted to increase the aperture of the lens.
Let’s think about this lens design conceptually. If we add a positive lens to the front side, the two positive lenses increase in overall optical power about the stop, so that means that the distortion becomes more difficult to correct. The last positive lens is moved farther away from the stop, in an attempt to correct the distortion.
The second lens is changed to an Aplanatic shape to minimize the aberration.
From the information in this guide, we can clearly see Bertele’s intentions, it’s like we’re reading his mind!
Another thing we notice is that the symmetry about the stop is lower in this design, so the field of view is narrower. However, a lot of the aberrations were corrected and it was possible to make a lens with an F-number of F2, which at the time (remember, this is the 1920’s) made for a lens with an extremely large aperture.
Ernemann was later merged alongside three other companies (Ica, Görz, and Contessa-Nettel) by Carl Zeiss in 1926, and Bertele designed spectacular lenses like the Sonnar and the Biogon.
Even today, a lot of medium telephoto lenses share characteristics with the Ernostar.
The Tessar
Another example, is the Tessar. The Golden age of Carl Zeiss was in part because of this lens. The Tessar name comes from Tetra, or the Greek word for the number four, since it has four lenses. Everyone remembers Tetris, right?
At first glance, the Tessar looks like a triplet with the last positive lens as a doublet. According to Carl Zeiss, the Tessar is the front group of the Unar, and the back group of the Protar, but I think there could have been some bureaucratic reasons for this explanation (sorry Paul).
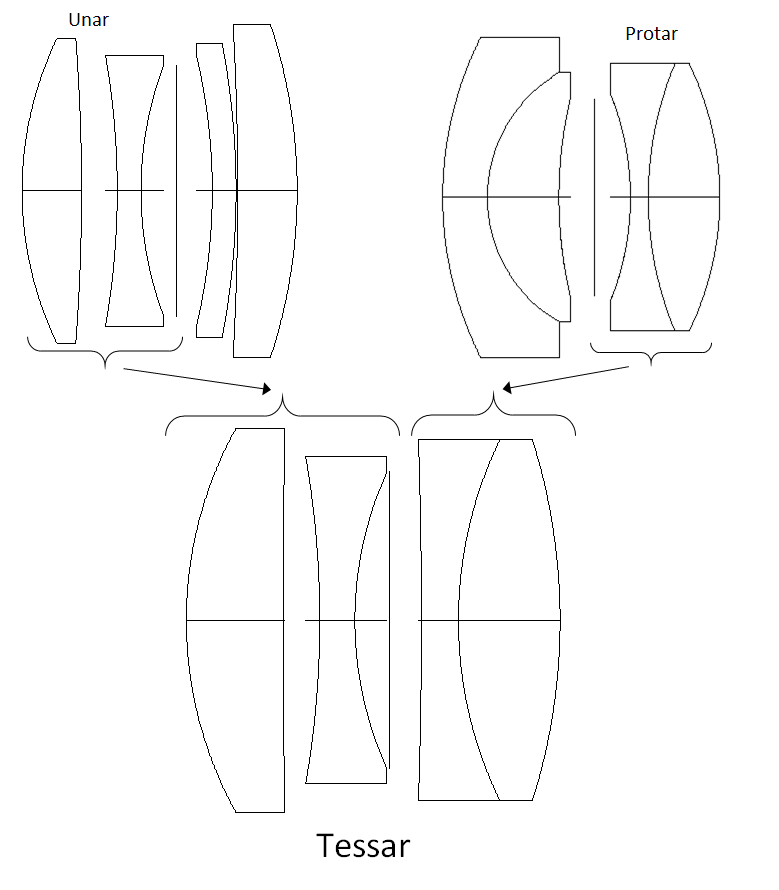
Optically speaking, assuming that the Tessar is an extension of the triplet makes it easier to understand, so I’m going to ignore Zeiss’ press release copy 😉
This lens form is relatively simple to implement, and we can add a cemented doublet in place of the last positive lens in the triplet. This last doublet is not for chromatic aberration correction, nor is it for spherical aberration correction, like we saw with the telescope objective. I had this preconceived notion that a cemented doublet, boom, that means colour correction.
If the doublet were for chromatic aberration, the data shows that the Abbe number of the lenses (51.0, 53.9) are too close to effectively correct colour.
If the doublet were for spherical aberration correction, the index of refraction of the positive element of the cemented double lens should be smaller than the negative element. But with close examination we can see that it is the opposite of a telescope objective.
We now know this after going through this guide.
Well, then what is that doublet for? We’ve mentioned before that the triplet has a limit to the astigmatism correction, and this doublet corrects the astigmatism at higher fields of view. This instantly makes the overall image much sharper from corner to corner compared to the triplet.
The same concept with a higher symmetry about the stop is the Heliar.
As a side note, the patent of the Tessar (USP721240) has the stop in between the negative lens and the doublet. The Ernst Leitz lens Elmar is a Tessar type which has the stop in between the first positive lens and the negative lens.

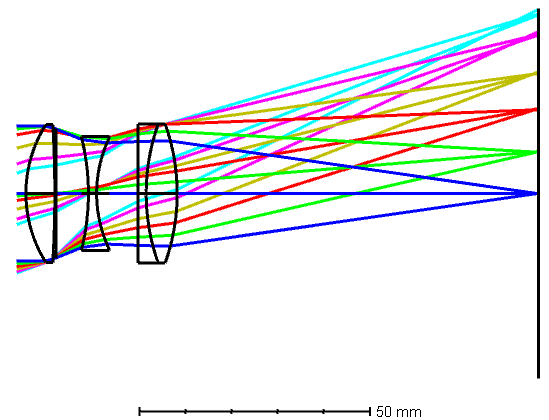
The Tessar was heralded as a superb lens compared to the triplet, with lower distortion, beautiful bokeh, and sharp image at the focus. With the marketing copy of “Das Adlerauge Ihrer Kamera – The Eagle Eye of your Camera”, many photographers worldwide used this lens.
By the way, a great resource for patents to look at in Zemax is www.lens-design.com, a file exchange site for lens designs. Via the website:
A library of lens designs is helpful for the optical engineer. Tasks that can benefit from such a library include choosing a starting point for a new design, finding benchmarks for an existing design, and assessing design targets.

This is a camera that I found at my grandfather’s house. I’d like to be able to use the lens for photography some day.
The Sonnar
While Paul Rudolph of Carl Zeiss designed the Tessar, Max Berek of Ernst Leitz designed the Elmar, and the performance was neck and neck. The camera was either a Contax or a Leica. Anything from an F-number of F3.5 to F4.5. The Elmar was nice due to the collapsing lens barrel for compactness, the Tessar was preferred for medium format photography. If there was a difference, Carl Zeiss lenses preferred overall performance across the entire image plane, while Leica preferred the center performance.
Smaller format cameras at the time (1920s – 1930s) were fighting for larger aperture of the lens. The reasons were twofold. One, the emulsion of film required for low sensitivity in the image plane (ISO in today’s terms), so the faster lens make for shorter shutter speeds and less hand-held blur. This was an advantage of smaller format cameras in terms of portability, compared to tripod-laden large format cameras at the time. Second, the focal lengths for smaller format cameras are shorter for the same field of view (35mm equivalent, in today’s terms) allowing for more depth of field with a larger aperture lens, with the same field of view.
I know, in the modern era where the “Full Frame” sensor is king, it’s hard to think that this format was considered small.
And yes, I know, it’s weird to think that back in the day, photographers wanted MORE depth of field, not less.
Long story short, for smaller format cameras a larger aperture normal lens was a game changer.
Then came the Sonnar. The genius Ludwig Bertele strikes again.
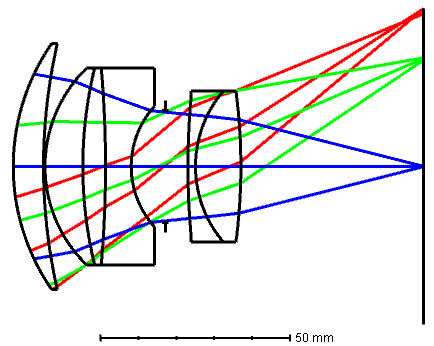
The Ernostar above made large apertures possible, but the large asymmetry caused coma. Therefore, the field of view for a normal lens, about 50mm focal length for 35mm format, was not possible. Also, without antireflective coating technology at the time, the more glass-to-air surfaces there were, there was more flare, and the transmission and contrast of the image decreased.
So Bertele took the Ernostar, filled the positive and negative lens in the front with another glass. This decreased the number of the glass-to-air surfaces to the same number as the triplet and the Tessar (six), while generating higher order spherical aberration (which we haven’t discussed in detail) for balancing. This allowed for shortening the overall length of the lens while keeping the large aperture intact.
Also, Bertele added the same doublet in the final group, much like the Tessar. We’ve already mentioned that this allows for a better image at larger fields of view, which means that the focal length can be shortened from the medium-telephoto Ernostar to the normal focal length Sonnar.
The lens ended up having an aperture of F1.5. The emergence of this lens must have made the competition wet their pants.
Today, the Sonnar isn’t as featured as THE standard for a normal lens. The Double Gauss has taken over, mainly due to a few factors.
1) The F1.5 Sonnar has more coma at higher field.
2) The development of higher index of refraction glasses allowed for better performance of the Double Gauss.
3) The anti-reflective coating technology was introduced and got better, the glass-to-air surface disadvantage was nullified.
4) The Sonnar has a short back focal length that doesn’t allow space for a mirror, and as SLRs took off in the 1960s, the Sonnar as a normal focal length lens didn’t take off with it.
However, one of my favourite lenses is the Sonnetar from MS-Optical. It is has a lot of spherical aberration and flare in the image that gives me a dreamy, creamy, look.

Going forward
There we go! We found out that expensive software is only a fraction of lens design. If software were a prerequisite, then lens design wouldn’t have become what it is today.
I’m not going to sit here and tell you that now you’re a master designer and give you a false sense of mastery. I also don’t want you to abandon software altogether. I certainly would’t.
Lens design, like any other skill, needs to be sharpened and improved with time. But I truly believe that we can all get there, with enough persistence. If we can help each other along the way, there wouldn’t be anything that would make me happier.
With the knowledge of our spreadsheet lens design and 3rd order aberrations, just looking at different lenses gives us an idea of the design concepts behind them. More importantly, it gives us an idea of the limits of the design, and we can make decisions based on our knowledge.
It turns out that our ability to design lenses in the modern era is based on our knowledge of the great designs of the past.
With practice, we can explain why our complicated multi-lens zoom lens requires this exotic lens here, and why our design is better than the current design, and where it lacks, because having 38 lenses in the system is a combination of correcting the aberrations.
Want to download the spreadsheets that I used for this guide to do lens design yourself? Go for it, just download it here!
In the meantime, what was your biggest takeaway with spreadsheet lens design? I’d really like to know.

Get Your FREE Lens Design Guide with Spreadsheets
Enter your name and email for instant access to our Guide to Classic Lens Design (in PDF format) and the actual spreadsheets used in the guide!
??100% privacy, and we hate spam. When you sign up, we'll keep you updated usually with one email per week, occasionally up to a few times a week. Unsubscribe at any time.
Special Thanks
Special thanks goes to:
- Primoz B. for providing the method that became the foundation to this guide. I truly could not have done this without you.
- Matej C. for the multiple one-on-one sessions that pushed me forward to get this project done. You are awesome!
- Megan C., Rinze K., and many others that helped with the editing and content of the guide. Your constant encouragement and willingness to help made the hard days easier.
P.S. If you enjoyed this guide, I’d LOVE it if you shared it on Facebook – on your own wall or in an online community you’re a part of, Twitter, Instagram. If you can also email it to a friend that would benefit from the concept of this Guide, it’ll make me double happy.
P.P.S. If you found this guide useful, leave a comment below to let me know what you found most useful! And if you have any questions, leave a comment as well – it would be my pleasure to answer all the questions in the comments section!
References:
- Field Guide to Geometrical Optics, John E. Greivenkamp, SPIE Press 2004
- Field Guide to Lens Design, Julie Bentley, Craig Olson, SPIE Press 2012
- Applied Optics and Optical Design Part 1 and Part 2, A. E. Conrady, Dover Publications 2011
- Lens design Fundamentals, Rudolf Kingslake, Academic Press 1978
- Optics 4th Edition, Eugene Hecht, Addison Wesley 2001
- Lens Design Methods, Yoshiya Matsui, Kyoritsu Press 1972 (Japanese)
- Lens Design Engineering, Jihei Nakagawa, Tokai University Press 1986 (Japanese)
- Modern Lens Design, Warren J. Smith, McGraw-Hill Education 2004
- Optical System Design Robert Fischer, McGraw-Hill Education 2008
- Introduction to Lens Design: With Practical Zemax Examples, Joseph Geary, Willmann-Bell 2002
- Aberrations of Thin Lenses, H. H. Emsley, Constable and Co Limited 1956
Great tutorial. I’m still getting my head around it. I’m getting an annoying result with a lens design and I was wondering if you could either explain what is the actual issue and, if possible, point me in the right direction to solve the issue. I can send you some screenshots of the beam profile depicting the issue once I have your email. The setup is basically an optic fiber and a single lens to achieve a specific beam spot size.
I’m enjoying you lens design guide. On my second pass I may have found a matrix factoring error.
Please check: Cooke triplet and anastigmat lenses, Section 4, subsection 2, the second row of the A matrix.
I think it should be [y1²/v1 y2²/v2 y3²/v3]. If I’m wrong please show me why.
Thanks