Comparison of the Double Gauss and Sonnar lens designs.

Do you think that lens design is all math, with complex equations and multiple calculations?

That’s only partly true.

There is another aspect of lens design that requires intuition, experience, and an “eye” for good performance. A more qualitative approach to the lens design that is a bit lost.

I want to compare two lens design forms that are completely different lens designs that tried to solve the same problem: A fast, all-purpose normal focal length lens for the 35mm format camera. Let’s dive in!

Introduction

The normal lens. The lens with a close field of view (FOV) to your vision.

The FOV is about 40 to 60 degrees.

There are two main optical lens design forms that competed for the top spot of the normal lens in the formative years of photographic cameras for lenses.

Here’s a quick recap of the two major competing lens design forms post-WWII.

• The Double Gauss lens
• The Sonnar lens

You’ll find articles and photos on the internet that compare the pre-war Sonnars, and even current Double Gauss and Sonnar comparisons.

I want to take a crack at the optical lens design aspect of the Double Gauss and the Sonnar, so let’s take a closer look at each with some hard data and graphs.

Double Gauss lens example

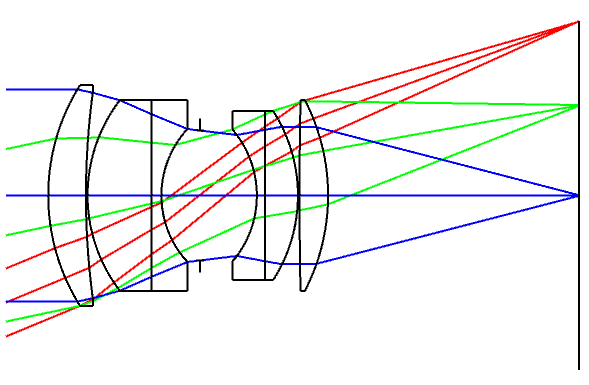
Focal length: \( f = 100 \)
Aperture ratio: 1:2
Back focal length: 59.21
Field angle: \( \pm 22.5 \deg \)

no.	R	t	n	\( \nu \)
1	+48.88	8.89	1.62286	60.08
2	+182.96	0.38	1.0	–
3	+36.92	15.11	1.58565	46.17
4	\( \infty \)	2.31	1.67764	31.97
5	+23.06	9.14	1.0	–
6(stop)	\( \infty \)	13.36	1.0	–
7	-23.91	1.92	1.57046	42.56
8	\( \infty \)	7.77	1.64128	55.15
9	-36.92	0.38	1.0	–
10	+1063.24	6.73	1.62286	60.08
11	-48.88	59.21	1.0	–

(Where no. is the surface number, R is the radius of curvature, n is the index of refraction, and \( \nu \) is the Abbe number)

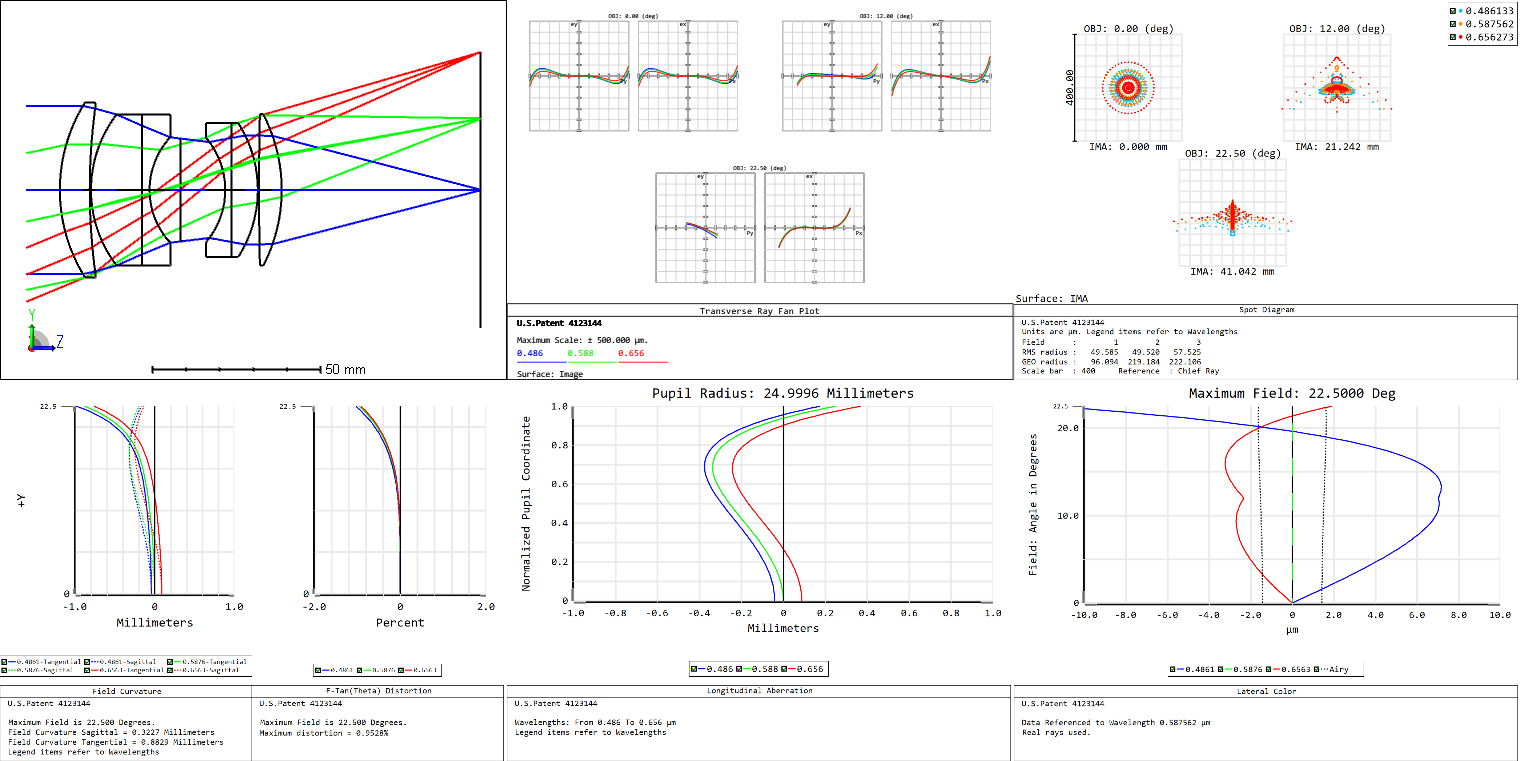
(click to enlarge)
(Top, from left to right: Lens layout, Ray fan, Spot diagram)
(Bottom, from left to right: Field curvature, Distortion, Longitudinal aberration, Lateral colour)

Sonnar lens example

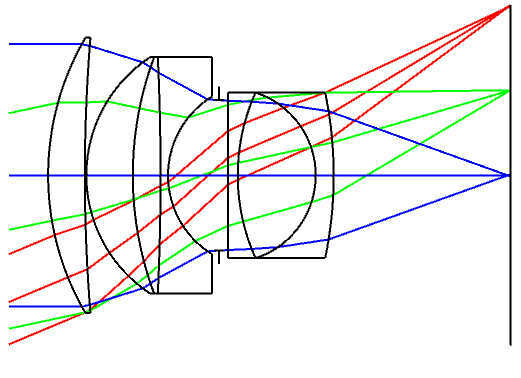
Focal length: \( f = 100 \)
Aperture ratio: 1:2
Back focal length: 44.90
Field angle: \( \pm 22.5 \deg \)

no.	R	t	n	\( \nu \)
1	+69.21	9.33	1.6710	47.2
2	+433.84	0.38	1.0	–
3	+35.86	11.81	1.6710	47.2
4	+85.87	7.05	1.4892	70.1
5	-646.31	1.90	1.7394	28.2
6	+23.51	13.00	1.0	–
7(stop)	\( \infty \)	2.24	1.0	–
8	\( \infty \)	2.48	1.5232	50.9
9	51.09	19.81	1.6578	51.2
10	-22.12	4.57	1.5894	61.2
11	-103.13	44.90	1.0	–

(Where no. is the surface number, R is the radius of curvature, n is the index of refraction, and \( \nu \) is the Abbe number)

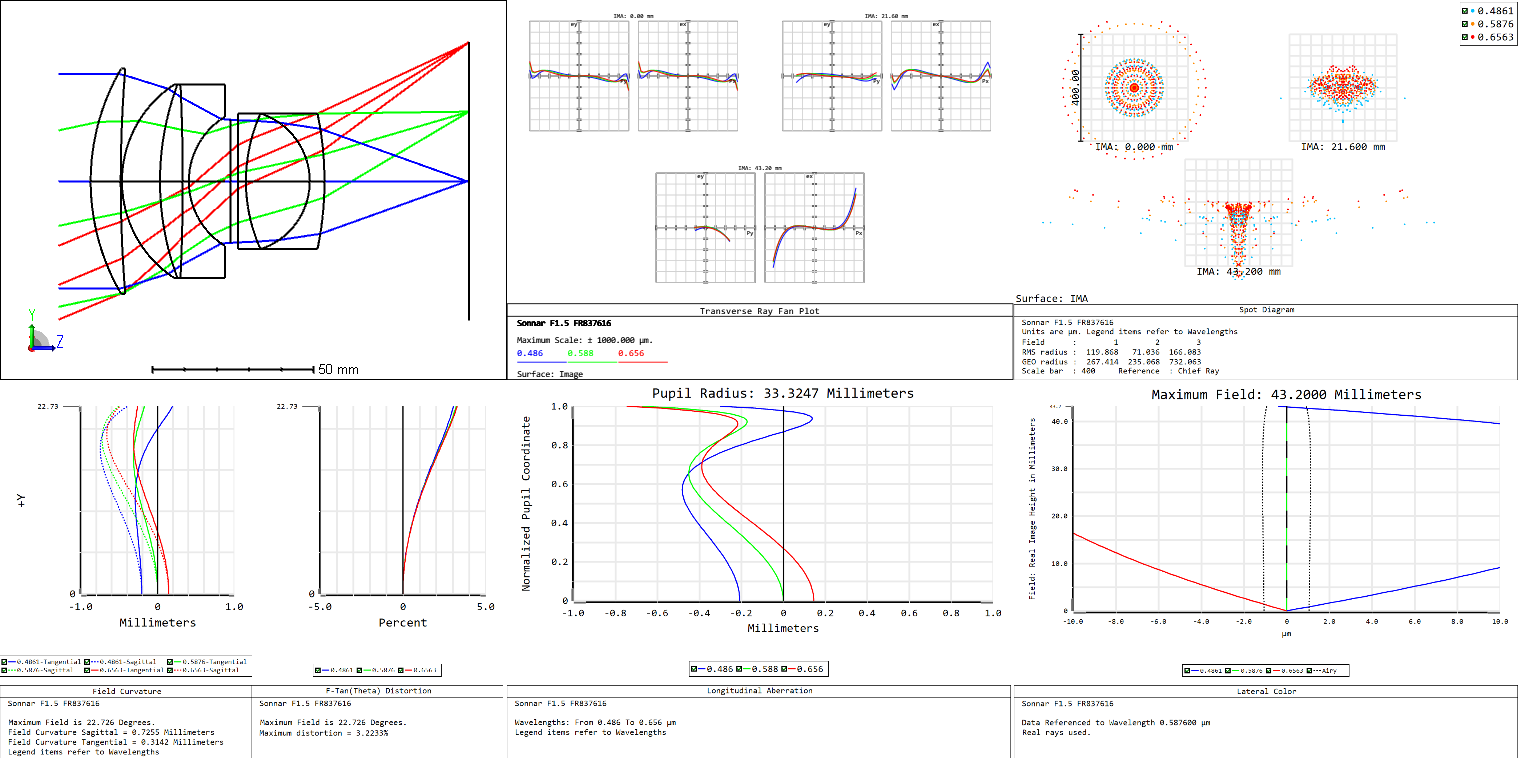
(click to enlarge)
(Top, from left to right: Lens layout, Ray fan, Spot diagram)
(Bottom, from left to right: Field curvature, Distortion, Longitudinal aberration, Lateral colour)

Both normal lenses with a manageable field of view, and both fast aperture (small f-number), which allowed for more light gathering for photography in dark situations.

There are similarities and differences between the two competing lenses, so let’s compare the two qualitatively, to train our eye for lens design, and for fun (well, it’s fun for me, at least).

Background of the Double Gauss lens and its multiple lens designers

By Paul1513 at en.wikipedia, CC BY-SA 3.0, Link

The Double Gauss lens was designed by Paul Rudolph, but its origin goes back a little bit.

The great mathematician Gauss and his lens

You may be thinking why this lens was named after the great mathematician Carl Friedrich Gauss. Gauss designed a telescope objective that comprised of two meniscus lenses, one positive meniscus and another negative meniscus, presumably to decrease the spherical aberration and longitudinal chromatic aberration by splitting one positive lens into two, preserving the overall power of the lens, but decreasing the curvature into four surfaces instead of two.

However, the Gauss lens does not correct the coma, and therefore does not meet the sine condition, was not popular among telescope objectives.

A bit later in 1888, Alvan Clark designed a lens that was a combination of two Gauss objectives flipped facing each other in a symmetric way. This made the lens better with the potential to become a photographic lens, but it was still limited to very slow apertures like F8.

Paul Rudolph and the Carl Zeiss Planar lens

The Double Gauss as we know it today was designed by Paul Rudolph, who recognized that the Clarke design was flawed but had potential. Rudolph attempted to correct the Petzval sum to correct the field curvature of the lens by thickening the inner meniscus lenses but found that this increases the chromatic aberration.

By making the negative meniscus lens a cemented hyperchromatic lens, Rudolph was able to correct the chromatic aberration to complete the first design of the Double Gauss lens.

A hyperchromatic lens is a cemented doublet lens that has the same index of refraction at the primary wavelength, but different dispersion or Abbe number. The characteristic of this lens is that by changing the radius of curvature of the cemented surface does not change the focal length of the primary wavelength, but changes the chromatic aberration. This is an effective way to think about chromatic aberration correction.

One aberration that the Double Gauss does not correct well is the coma.

How technological innovation lead to breakthroughs in the Double Gauss lens performance

Early attempts to improve the Double Gauss lens design

There were many lens designers that attempted to improve coma of the Double Gauss design over the years, some by adding more cemented surfaces to the negative lenses with a triplet and creating a strong curvature of the cemented surface (Warmischam, USP 2130760), some by making the first lens a cemented lens and breaking the symmetry (Berek, Polish Patent 685572), some by splitting the positive lenses (Lee, USP 2019985). All this in an attempt to correct the coma, with mixed results and no conclusive solutions.

How high index of refraction, low dispersion glass changed the Double Gauss lens design

It wasn’t until the emergence of higher index glass with lower dispersion could the coma be corrected. Bonus points for the possibility of a faster aperture and smaller Petzval sum (better field curvature).

The invention of low dispersion, high index glass, anti-reflective coatings, and computational lens design provided for a breakthrough in the lens design of the Double Gauss lens.

Walter Mandler’s Summicron designed for the Leica is the pinnacle of the Double Gauss in my opinion. Sure, there are better performing Double Gauss lenses with a faster aperture, but the fact that this lens was sold for nearly forty years without an update until the most recent Apo-Summicron (with an aspherical surface) that there was a major update to this lens.

Walter Mandler’s Leitz Summicron design, US4123144 (1976)

Further variations on Double Gauss lens design

Another method of improving the Double Gauss design was to split the front doublet in two. By doing this it is possible to decrease the coma since the concave surface right after the stop also decreases. This was only an option after anti-reflective coatings were invented, since more air-to-glass surfaces meant that there was less transmission of the lens and decreased the contrast in the image.

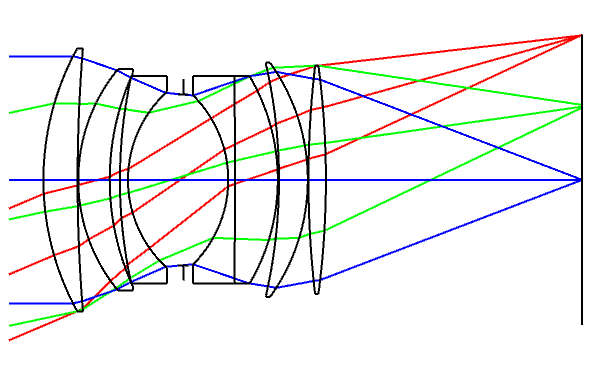
Nikkor design, Wakiyama US4448497 (1981)

Even further to modern times, most Double Gauss variations have a retrofocus-like look to them.

Background of the Sonnar and Ludwig Bertele, lens design genius

The Sonnar was designed by one of my lens design heroes, Ludwig Bertele.

Ludwig Bertele worked at Ernemann, and later Cal Zeiss, when Ernemann was later merged alongside three other companies (Ica, Görz, and Contessa-Nettel) in 1926.

From what I can tell, Bertele is nothing short of a genius. He made very bright F-number lenses in a time where anti-reflective coatings did not exist, and in a time when glass choices were still primitive.

The Ernostar lens, precursor to the Sonnar

Bertele took the triplet design, and added an aplanatic lens in between the first and second lenses in order to decrease the spherical aberration. The result was an extremely fast lens for its time, an F2 lens with well corrected spherical aberration and chromatic aberration.

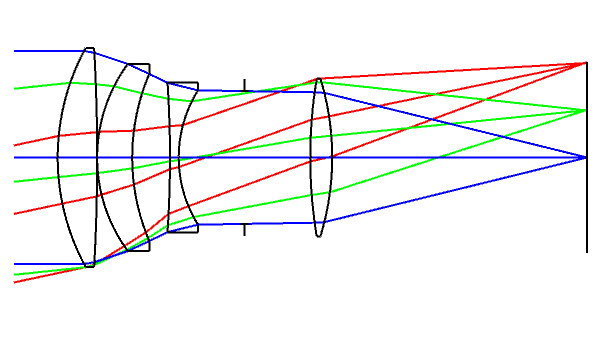
Ludwig Bertele’s Ernostar design, GB237212 (1925)

This innovative lens design stands the test of time, as the Ernostar is a great starting point for longer focal length lenses.

But the Ernostar had some problems. The field curvature was not well corrected, hence the above use for longer focal lengths (narrow field of view).

The Sonnar was Bertele’s next lens innovative lens design while in Zeiss, he packed the air gap in between the second and third lens of the Ernostar to avoid Fresnel loss (no anti-reflective coatings at the time). He further made the last element a doublet, much like Paul Rudolph’s Tessar. This doublet helped correct the oblique aberrations such as field curvature, and thus higher fields of view. Higher field of view means shorter focal length, so the previous long focal length Ernostar was able to be a normal lens.

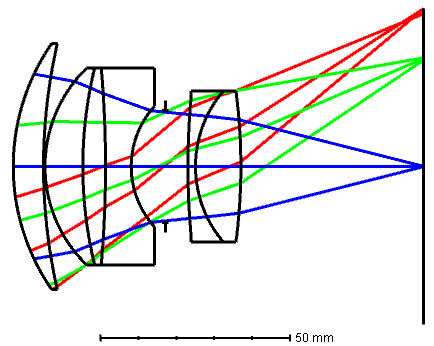
Ludwig Bertele’s Sonnar design, DE570983 (1931)

A little bit more on Bertele

By Anonymous – en:wikipedia, CC BY-SA 3.0, Link

While in Carl Zeiss, Bertele continued to design spectacular lenses like the Sonnar F1.5 and the Biogon, both which I think are not only lenses that perform beautifully, but also look beautiful as a lens diagram. I think his lens designs as the leading technology of the time.

Ludwig Bertele’s Sonnar F1.5 design, FR837616 (1937)

Bertele also designed eyepieces, in an age when Erfle types were thought of as the pinnacle of eyepiece design. This was the time that Zeiss binoculars had their post-war resurgence. Bertele’s binocular eyepieces look more like photographic lenses than eyepiece glass.

Bertele left Zeiss in 1942, worked at Steinheil for a brief while and then retired but still did lens design in his seventies on a consulting basis.

One thing about Bertele that I find fascinating is that he neither wrote any academic papers or books. Such a genius level lens designer didn’t feel the need to document his iconic ideas on lens design.

When I look at Bertele’s patents, I can see the level of work he put into his designs. The variations in his lens designs in his patents are simple but thorough.

I have read a few snippets about Bertele, and his later years in lens design. For example, he knew about aberration theory but didn’t use it at all. Also, he used a primitive computer and insisted that automatic lens design was useless. He never published a book or scientific papers of his lens design process and knowledge, so we can only sit here and imagine his lens design process.

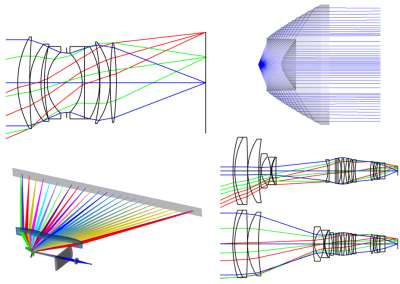
Deep dive into the comparison between the Double Gauss and the Sonnar

Now that we know a little bit about the two lenses, let’s compare the performance of the two. Let’s look at the performance of the two again.

(click to enlarge)
(Top, from left to right: Lens layout, Ray fan, Spot diagram)
(Bottom, from left to right: Field curvature, Distortion, Longitudinal aberration, Lateral colour)

(click to enlarge)
(Top, from left to right: Lens layout, Ray fan, Spot diagram)
(Bottom, from left to right: Field curvature, Distortion, Longitudinal aberration, Lateral colour)

The Double Gauss has a long back focal length, the Sonnar has better spherical aberration correction

• Since the Double Gauss is closer in symmetry, the coma, distortion, and transverse chromatic aberration is easier to correct, and the back focal length is long.
• For the F1.5 type Sonnar, the rear elements have to have a strong curvature, resulting in thicker lenses. The Sonnar also has a shorter back focal length. While in the age of rangefinder cameras and before coatings were invented the Sonnar was the champion of lenses, but in the SLR era, the Double Gauss lens took its championship belt.
• Of course, at longer focal lengths, like 85mm or 135mm, the total length is short and the higher field aberrations have less of an effect to the performance. In a sense, the Sonnar can be seen as in between the Petzval lens and the Double Gauss lens, in terms of the aberrations it can correct.

The cemented elements have the same job, they both correct the aberrations at higher field

• The cemented 5th and 6th lenses in the Sonnar, and the 4th and 5th lenses in the Double Gauss, both have a positive lens that has a higher index of refraction. This is to correct the aberrations at a higher field of view, much like the Tessar lens.

The Double Gauss has sagittal aberrations

• The aberration is caused by the concave surface on the negative lens. This is also the reason why the back focal length is long, which helps for SLR cameras.
• The Sonnar has very good sagittal aberration correction.
• Back in this time, the calculations for skew rays and spot diagrams would take too long to do.

The front element generates high order spherical aberration for correction

• We can see that the curved cemented surface in between the 2nd and 3rd lens for the Sonnar doesn’t affect the marginal rays nor the chief ray too much, and is almost a dummy surface. The cemented surface in between the 3rd and 4th lens, although relatively flat, has converging rays and changes incident angles as the field increases. Since the 4th lens is negative and has a high index of refraction, this causes an overcorrection of the higher order spherical aberration.
• Similarly for the Double Gauss lens, the higher-order spherical aberrations are generated with the 2nd and 3rd lens, but the Sonnar can achieve this at a higher level without relying on a glass with a higher index of refraction out of the norm.
• The best 3rd lens for the job would be an air space, but Bertele introduced a low index low dispersion glass to reduce the number of air surfaces since coatings weren’t invented yet. The Cosina Sonnar does exactly this, with the advancements in coating technology this was the real lens form that Bertele would have wanted.

The Sonnar F1.5 has an interesting rear group of lens elements

• It was a high index of refraction for the positive lens, and undercorrects the spherical aberration. The index difference is not large, and includes a surface with a high curvature. These elements cause the 7th order aberration.

What do you think? Was there any complex math involved? Granted, there are some analysis (such as the aberration generation of each surface) that I didn’t show, but as long as we understand how the aberrations occur within the lens design by looking closely at the surfaces and glass types, we can get a good idea of the lens design concepts that make these lenses work the way that they do. In turn, we can take that knowledge and use it to our advantage in our own lens designs.

The lens design battle between the Double Gauss and the Sonnar

The Double Gauss was around first in the form of the Carl Zeiss Planar, and adopted by many lens companies. The Sonnar came around a quarter-century later on the Zeiss Contax as its normal lens.

In the beginning, the Contax with the Sonnar outperformed the Leica, since Leica relied on Double Gauss lens forms for its normal lenses. In an age with few high index glass and no anti-reflective coatings, the Sonnar F2 lens was the better performer.

Only until low dispersion high index glass and anti-reflective coatings did the Double Gauss catch up with the Sonnar.

Eventually, the rise of single reflex mirror cameras over the rangefinder camera marked the doom for the Sonnar.

The mirror in the camera required a longer back focal length of the lens, which the Sonnar could not provide. The Double Gauss lens, with some slight asymmetry, could increase the back focal length to accommodate the flapping mirror.

The Sonnar continued to sell with variants in fixed lens compact cameras and lenses for newer rangefinder cameras, but largely became a shadow in the dominant Double Gauss landscape we have today.

Why training the lens design eye is important

In summary, all of the technical insights were made by “looking” at the lens intelligently, no hard math, no involved calculations. This is the benefit of training the eye in lens design.

I think that just having the lens diagram is very limiting information. The lens diagram, coupled with a few rays like the marginal ray and the chief ray, gives us much more information. In addition, the index of refraction and dispersion shows us which side of the cemented lens has a higher index and by how much, which leads to more insightful lens design concept analysis.

The lens form is like a road, and the ray path is the automobile. We need both to find the best lens form for the job. Explaining lens design with just the lens diagram, without the rays and index data, is like explaining how to drive with a roadmap and no automobile.

For more information on lens design, check out my Ultimate Guide to Lens Design Using the Classic Spreadsheet Method, where I explain how you can learn lens design without expensive proprietary software.

For more information on lens design and lens design forms, check out my Ultimate Guide to Lens Design Forms, where I break down over 50 lens design forms so you know which lens is used for what situation and why.